Crypto学习总结
本文最后更新于:2023年11月15日 下午
RSA
from Crypto.Util.number import *
from gmpy2 import *
- 导入两个经典的模块
d = inverse(e, phi)
d = invert(e, phi)
inverse函数,invert函数,函数有两个参数(a,p),作用便是求解a在模p意义下的乘法逆元,- 这里我们便是求解
e在模phi下面的乘法逆元,结果为d - 即满足$ e* d ≡ 1(modφ(n)) $
- 即满足$ (d * e) % phi = 1 $,%的意思是取余
- 这个语句使用的是
Crypto.Util.number模块中的inverse()函数
d = gmpy2.invert(e, phi)
- 该函数计算了一个整数 e 的模逆,也就是找到一个整数 d,使得$ (d * e) % phi = 1 $
- 也即是
d * e ≡ 1 (mod phi) - 这个语句使用的是外部库
gmpy2的invert()函数来计算乘法逆元,gmpy2和Crypto中的数学函数相比:二者速度不是一个量级。
d = pow(e,-1,phi)
- 当传递三个参数时,
pow(x, y, z)用于计算x的y次幂模z的结果。在这里,e是底数,-1是指数,phi是模数。通过将指数设置为-1,pow(e, -1, phi)计算了e的模phi的乘法逆元。 - 这个语句使用的是内置函数
pow()来执行指数运算和模计算。
a = powmod(a, m, n)
powmod(a, m, n)与pow(a, m, n)效果一样
gmpy2.iroot(x, n)
- 其中,
x是待计算根号的整数,n是根号类型的整数值。irrot(c,e)表示 对c开e次根号, - 如果
x的根号为整数,函数将返回一个元组(tuple),返回值为(mpz(2), False),第一个参数表示返回的结果,mpz为gmpy2包中对整数的封装类,看作一个整数即可;第二个参数代表这个数是否能被完全开e次方,true表示能。 - 例如10开3次方并不是一个整数,但
gmpy2只会返回取整后的整数值,故通过第二项我们能够知道是否为完全k次方数。 - 例如
iroot(9, 2)返回(mpz(3), True)代表9是一个完全平方数。 - 如果想获得根号的整数值,可以通过访问元组的第一个元素来实现,例如:
m1 = gmpy2.iroot(m, 2)[0]print(long_to_bytes(m[0]))
- 也能直接赋值的时候就赋给两个变量,这里a就是取平方根后的整数值
a, b = gmpy2.iroot(m,2)
.\yafu-x64.exe "factor(@)" -batchfile 1.txt
- 分解1.txt中的整数
1 | |
快速解密
ciphey -t "4O595954494Q32515046324757595N534R52415653334357474R4N575955544R4O5N4Q46434S4O59474253464Q5N444R4Q51334557524O5N4S424944473542554O595N44534O324R49565746515532464O49345649564O464R4R494543504N35"
Windows安装ciphey编码工具,编码工具战神,cry简单题绝对克星!
第一个RSA,

那就了解一下RSA是什么吧,嘻嘻😍
一个简单的介绍视频RSA 算法基本原理_哔哩哔哩_bilibili
简单来说就是:
A把一个公钥(e,N)给B,B把想发给A的信息 m 用(e,N)加密成 c 后发给A,A有个私钥(d,N),用私钥解密即可,这里的 d 只有A掌握,别人很难知道(涉及大整数分解问题),所以方案安全。
就是保证了信息加密是容易的,而反向解密是困难的
过程再稍微稍微详细一点就是:
- 选两个大质数p和q,且p!=q,计算N=p*q,N就算出来了
- 然后计算N的欧拉函数 φ(N)=(p-1)(q-1)
- 然后你自己选个e, 1<e<φ(N),且与φ(N)互质,
- 由e和φ(N)互质,(e,φ(N))=1,再由辗转相除法,则一定有ed - φ(N)k = 1
- 那么由e就可以算出d,如下图(下图中的p1,p2就是p,q)
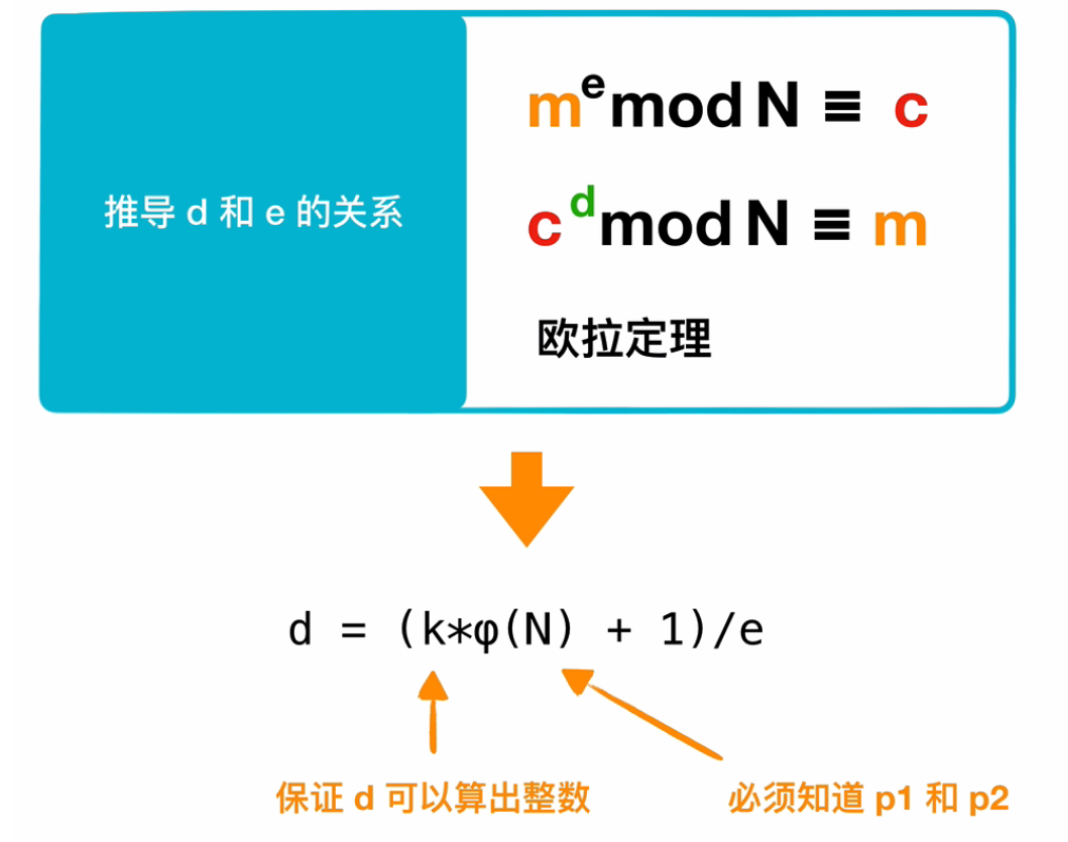
- enmmmm,就是这样🐌
下面是视频里面的一个小实例,帮助理解
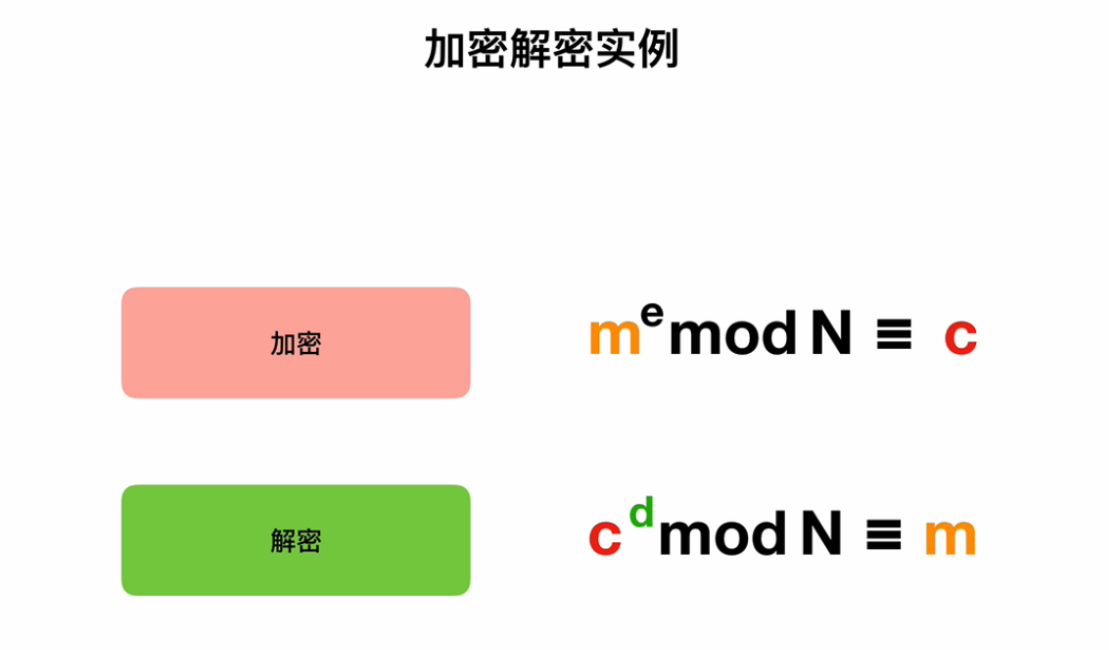
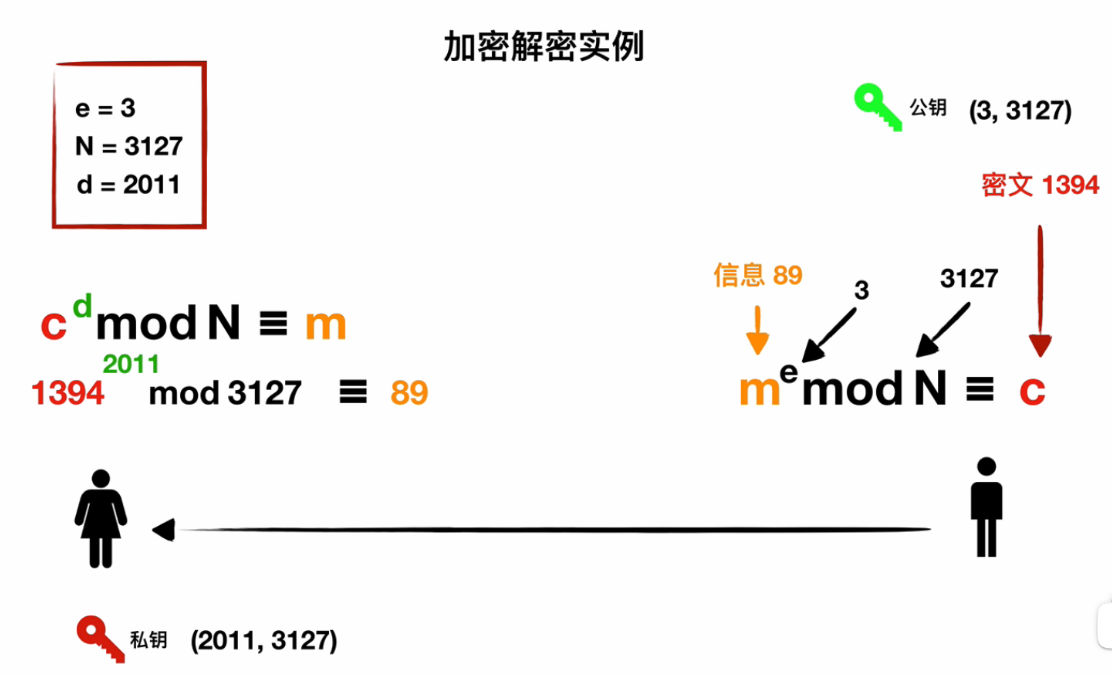
虽然有些原理还不太清楚,但学到现在这题基本就能解决了
1 | |
flag is : NSSCTF{08bb8fb628da85923e5734a75ac19ffe}
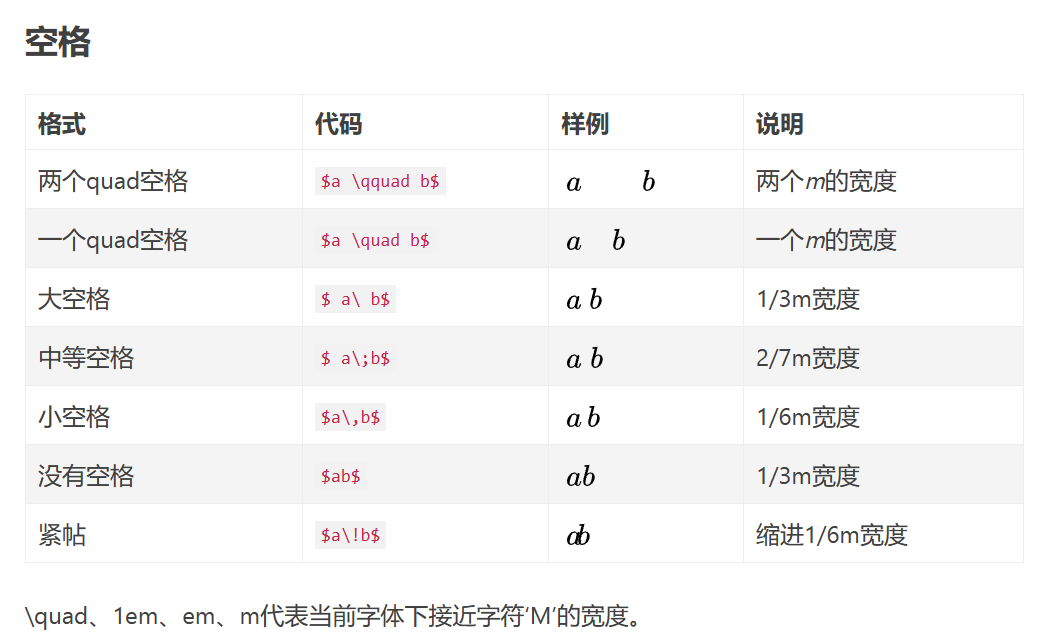
数学公式里面的空格
% 意思是打出一个%符号
% 单独输入这个可以把后面的都注释掉
写数学公式换行:
\(p=q\),$ p =q$,后面这个就显示错误,不能有空格
行的中间也不能有空行
[CSDN_Markdown] 数学公式对齐_markdown 数学公式对齐-CSDN博客