算法设计与分析-动态规划

本文最后更新于：2024年1月7日 晚上

多段图最短路径问题

1

动态规划法

动态规划法将待求解问题分解成若干个相互重叠的子问题，每个子问题对应决策过程的一个阶段，一般来说，子问题的重叠关系表现在对给定问题求解的递推关系(称为动态规划函数)中，将子问题的解求解一次并填入表中，当需要再次求解此子问题时，可以通过查表获得该子问题的解，从而避免了大量重复计算。具体的动态规划法多种多样，但都具有相同的填表形式。一般来说，动态规划法的求解过程由以下三个阶段组成：

  1. 划分子问题：将原问题分解为若干个子问题，每个子问题对应一个决策阶段，并且子问题之间具有重叠关系。
  2. 确定动态规划函数：根据子问题之间的重叠关系找到子问题满足的递推关系式即动态规划函数，这是动态规划法的关键。
  3. 填写表格：设计表格，以自底向上的方式计算各个子问题的解并填表，实现动态规划过程。

上述动态规划过程可以求得问题的最优值即目标函数的极值，如果要求出具体的最优解，通常在动态规划过程中记录必要的信息，再根据最优决策序列构造最优解。

多段图最短路径问题

设图 \(G =（V,E）\) 是一个带权有向图，如果把顶点集合 V 划分成 k 个互不相交的子集 \(V_i（2≤k≤n,1≤i≤k）\)，使得 E 中的任何一条边 <u,v>，必有 \(u∈V_i, v∈V_{i + m}(i<k, 1<i+m≤k)\),则称图 G 为多段图，称 s∈V1 为源点，t∈Vk 为终点。

多段图的最短路径问题为从源点到终点的最小代价路径，如下动图所示：

多段图是一个有向的无环图。求解从起始点到终止点的最短路径的长度， 首先看一下这个问题是否具有最优子结构的性质。对于每一点来说，从v0 到它的最短路径有两种可能，分别是从v0直接到该点或者是从最短的前驱节点开始到该节点。从这里可以看出有递归的性质，所以使用回溯的方法也是可以解决的。即从终点开始，依次向前找到最短的路径。由于递归本身所用的时间较长，并且在回溯的过程中存在重复的工作，所以使用动态规划更好。

2

最优子结构证明

适合采用动态规划方法的最优化问题中的两要素：

✓ 最优子结构

✓ 重叠子问题

一、 最优子结构

  • 如果问题的最优解是由其子问题的最优解来构造的，则称该问题具有最优子结构

  • 在动态规划中，我们利用子问题的最优解来构造问题的一个最优解，因此必须确保在我们所考虑的子问题范围中，包含了用于一个最优解的那些子问题

二、重叠子问题

  • 适用于动态规划求解的最优化问题的第二个要素是子问题的空间要小，使用来解原问题的递归算法可反复解同样的子问题，而不总在产生新的子问题。
  • 不同的子问题数是输入规模的一个多项式。
  • 递归算法求解问题时，每次产生的子问题并不总是新问题，有些子问题被反复计算多次，该性质称为子问题的重叠性质

设s，s，s1，s2，……，sp，t是s到t的一条最短路径，且s到s1的路径已经求出，则问题转为s1到t的最短路径，因此s1，s2，……，sp，t构成一条最短路径，如果不是，则设s1，r1，r2，……，rp，t是一条从s1到t的最短路径，则s，s1，r1，r2，……，rp，t是一条从s到t的最短路径且比s，s1，s2，……，sp，t短，因此矛盾，所以多段图的最短路径问题满足最优性原理。

问题分析

image-20231108235209001
image-20231109112545467

程序实现

c

arc[N] [N]：图的邻接矩阵 cost[N]：一维数组 存储到每个顶点的最小开销。

image-20231109114707374

path[N]：用来保存每个顶点的前驱顶点，注意这个前驱结点是最短路径上的

image-20231109114720321 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
#include <stdio.h>

#define N 100
#define MAX 999999

int arc[N][N];

int CreateGraph() {
    int i, j, k;
    int weight;
    int vnum, arcnum;

    printf("请输入顶点的个数: ");
    scanf("%d", &vnum);
    printf("请输入边的个数: ");
    scanf("%d", &arcnum);
    
     // 把arc初始化为一个vmun*vnum的矩阵，
    for (i = 1; i <= vnum; i++) {
        for (j = 1; j <= vnum; j++) {
            arc[i][j] = MAX;
        }
        arc[i][i] = 0; // 顶点到自身的距离为0
    }

    printf("请输入边的两个顶点和权值: \n");
    for (k = 0; k < arcnum; k++) {
        
        scanf("%d %d %d", &i, &j, &weight);
        arc[i][j] = weight;
    }

    return vnum;
}

//返回最短路径
void BackPath(int n) {
    int i, j;
    //cost[N]是一个一维数组表，用来存储源点到每个顶点的最小开销
    //path[N]保存每个结点的前驱
    int cost[N], path[N];

    //cost[i]初始化为长度为n的一维数组，值为arc[1][i]，即为源点到每个顶点的距离
    //path[i]，用来保存每个顶点的前驱顶点，先都初始化为1，后面不更新的话就是1->n，注意这个前驱结点是最短路径上的
    for (i = 1; i <= n; i++) {
        cost[i] = arc[1][i];
        path[i] = 1;
    }

//for i=2,因为第一行已经赋值给cost[i]了，所以只需要遍历n-1行即可

    for (i = 2; i <= n; i++) {
        for (j = 1; j <= n; j++) {
            // 检查是否存在一条从源点1经过顶点 i 到达顶点 j 的路径，其开销小于当前的 cost[j]，小于的话就更新cost[j]
            if (cost[i] + arc[i][j] < cost[j]) {
                cost[j] = arc[i][j] + cost[i];
                path[j] = i;   // 更新路径上的前一个顶点
            }
        }
    }
    
    for (i = 1; i <= n; i++) {
        printf("从顶点1到顶点%d的最小开销为：%d，路径为：", i, cost[i]);
        j = i;
        while (j != 1) {
            printf("%d <- ", j);  // 输出路径
            j = path[j];  // 回溯路径上的前一个顶点
        }
        printf("1\n");
    }
}

int main() {
    int vnum = CreateGraph();
    BackPath(vnum);
    return 0;
}

c++

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
//c++的代码的coppy，没学过c++，主要看思路，
#include<iostream>
#include<stdio.h>
#define MAXV 11
using namespace std;

typedef struct{    //图的定义
    int edges[MAXV][MAXV];    //邻接矩阵
    int n;    //顶点数
} MGraph;

MGraph topography;    //保存城市关系的邻接矩阵 
int path[MAXV] = {};    //保存到该顶点的最短路径对应的前驱 
int min_cost[MAXV] = {};    //保存到每个顶点的最短路径长 

MGraph CreateMGraph(int num)    //建图 
{
	// MGraph topography;
	int n;
	int point1, point2;
	int value;
	
	//初始化边为不存在 
	for(int i = 1; i <= num; i++){
		for(int j = 1; j <= num; j++){
			topography.edges[i][j] = 0;
		}
	}
	cout << "请输入边数：";
	cin >> n;
	for (int i = 0; i < n; i++){
		cin >> point1 >> point2 >> value;
		topography.edges[point1][point2] = value;
	}
	cout << "\n建立的邻接矩阵为：" << endl; 
	for(int i = 1; i <= num; i++){
		for(int j = 1; j <= num; j++){
			printf("%2d ",topography.edges[i][j]);
		}
		cout << endl;
	}
	cout << endl;
	topography.n = num;
	return topography;
}

int main(){
	int cities_num = 0;    //城市数量 
	int a_cost;    //当前路径的开销
	int pre;
	
	cout << "城市数量为："; 
	cin >> cities_num;
	//建图
	topography = CreateMGraph(cities_num);
        //初始化路径开销
	min_cost[1] = 0; 
	for(int i = 2; i <= topography.n; i++) {
		min_cost[i] = 99999;
	}
	//依次计算到达所有点的最短路径 
	for(int i = 2; i <= cities_num; i++){
		//遍历之前的所有点，计算到达该点的最短路径 
		for(int j = 1; j < i; j++){
			if(topography.edges[j][i] != 0){    //若路径存在 
				a_cost =  min_cost[j] + topography.edges[j][i];
				if(a_cost < min_cost[i]){    //更新最短路径长 
					min_cost[i] = a_cost;
					path[i] = j;    //记录前驱顶点 
				}
			}
		}
	}
	//输出到所有顶点的最短路径 
	for(int i = 1; i <= cities_num; i++){
		cout << "到顶点" << i << "的最小开销为：" << min_cost[i] << "，路径：" << i;
		pre = i;
		while(path[pre]){
			cout << "<-" << path[pre];
			pre = path[pre];
		}
		cout << endl;
	}
        return 0;
}

测试样例

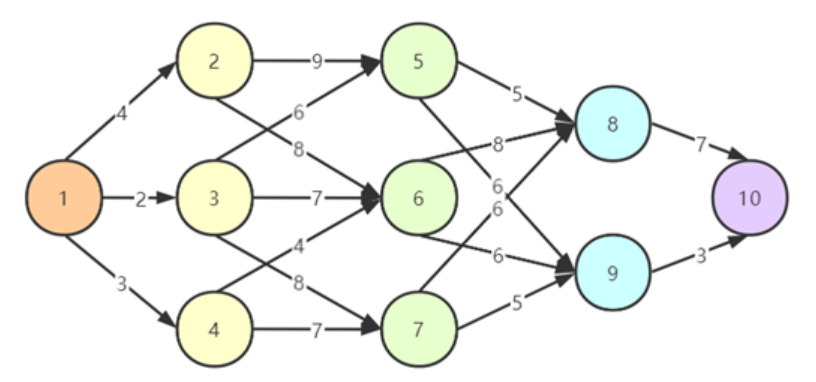image-20231108235209001

输入数据

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
10
18
1 2 4
1 3 2
1 4 3
2 5 9
2 6 8
3 5 6
3 6 7
3 7 8
4 6 4
4 7 7
5 8 5
5 9 6
6 8 8
6 9 6
7 8 6
7 9 5
8 10 7
9 10 3

输出数据

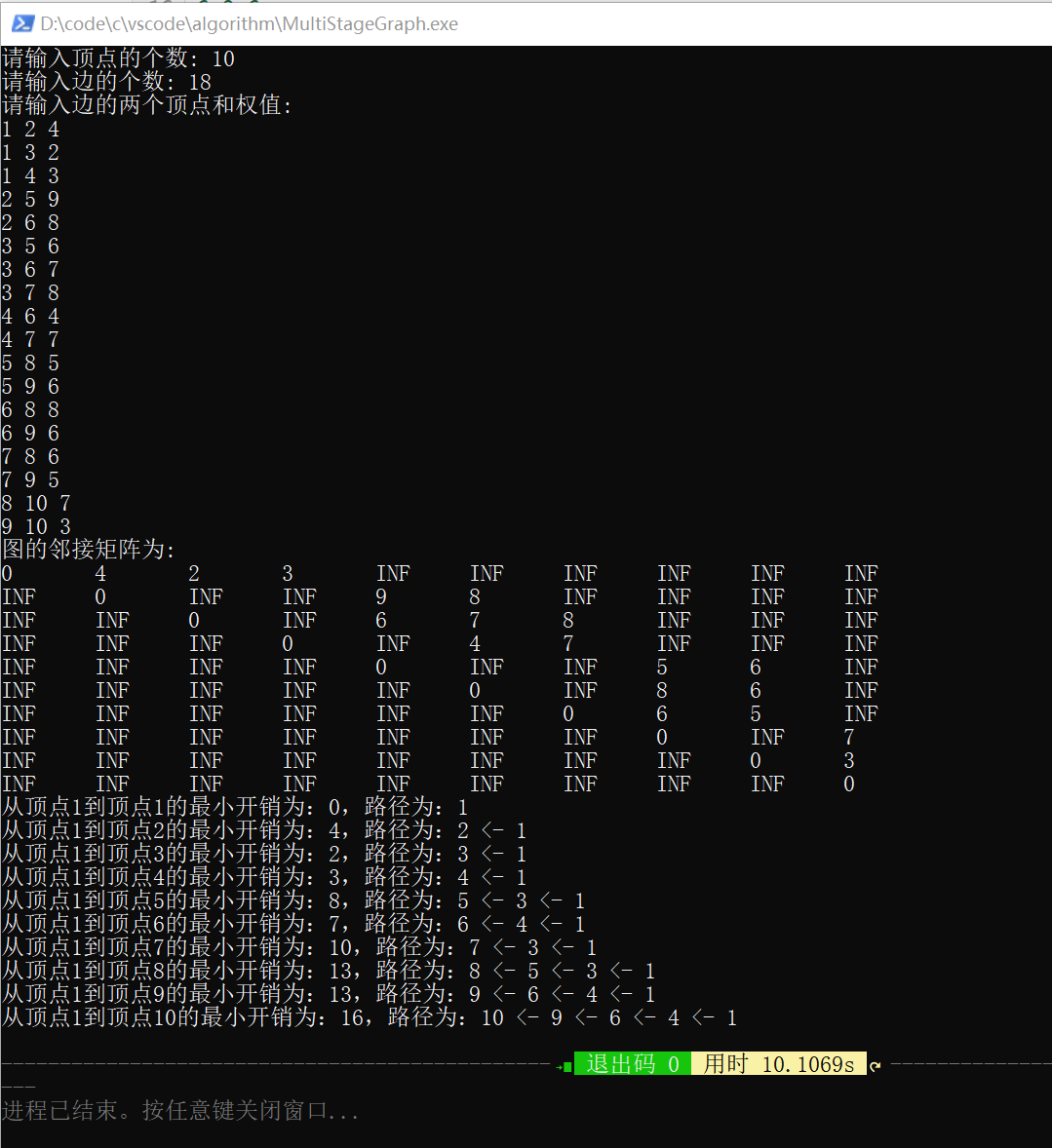image-20231109113255170

算法分析

算法的时间复杂度主要由两部分组成：

第一部分是依次计算从源点到各个顶点的最短路径长度，由两层嵌套的循环组成，外层循环执行 n-1 次，内层循环对所有入边进行计算，并且在所有循环中，每条入边只计算一次。假定图的边数为 m，则时间性能是 O(m)。

第二部分是输出最短路径经过的顶点，设多段图划分为 k 段，其时间性能是 O(k)。

综上所述，时间复杂度为 O(m+k)。

参考:

动态规划法解多段图最短路径问题 - 乌漆WhiteMoon - 博客园 (cnblogs.com)

【动态规划】多段图最短路径（动图演示）-阿里云开发者社区 (aliyun.com)

算法分析与设计
#算法 #动态规划
算法设计与分析-动态规划
http://viper2383.github.io/2023/09/18/算法 4-动态规划/
作者
w1per3
发布于
2023年9月18日
许可协议