数据结构学习

第二章 线性表

2.5

L=(LinkList)malloc(sizeof(LNode)); P=L;
for(i=1;i<=4;i++){
    P->next=(LinkList)malloc(sizeof(LNode));
	P=P->next; 
	P->data=i*2-1;
}
P->next=NULL;
for(i=4;i>=1;i--) Ins_LinkList(L,i+1,i*2);
for(i=1;i<=3;i++) Del_LinkList(L,i);

L=(LinkList)malloc(sizeof(LNode));

这行代码是C或C++中用于动态分配内存并创建一个链表（或链表的头节点）的代码。

这行代码作用的详细解释：

1. malloc 函数：malloc 是C和C++中用于动态分配内存的函数。它的作用是在堆（heap）中分配一块指定大小的内存，并返回一个指向该内存块的指针。在这里，malloc(sizeof(LNode)) 分配了一块大小为 sizeof(LNode) 字节的内存。
2. sizeof(LNode)：sizeof 是一个运算符，用于获取数据类型或结构体的大小（以字节为单位）。LNode 是链表节点的数据结构（或类型），因此 sizeof(LNode) 返回 LNode 结构体的大小。
3. (LinkList) 强制类型转换：在C和C++中，malloc 返回一个 void 指针，需要将其转换为所需的数据类型，这里是 LinkList 类型。这样做是为了让指针指向正确的数据类型，以便后续操作。
4. L：这是链表的头指针，它被分配了一块内存，并指向了链表的头节点。

总结起来，这行代码的作用是创建一个链表，并将链表的头指针 L 指向一个新分配的内存块，该内存块大小为 sizeof(LNode) 字节，用来存储链表的头节点。

这是创建链表的起始步骤，通常会跟随其他操作来构建链表的节点和连接。在使用完链表后，需要记得使用 free 函数来释放分配的内存，以避免内存泄漏。例如：free(L)。

for(i=1;i<=4;i++){
    P->next=(LinkList)malloc(sizeof(LNode));
	P=P->next; 
	P->data=i*2-1;
}

这段代码是一个循环，它用于在链表中创建四个节点，并为每个节点赋值。解释如下：

1. for(i=1;i<=4;i++)：这是一个循环，它会执行四次，i 从1开始，每次递增1，直到 i 的值为4。
2. P->next=(LinkList)malloc(sizeof(LNode));：这行代码分配了一个新的内存块，用于存储下一个节点，并将当前节点的 next 指针指向这个新节点。这意味着创建了一个新节点，并将其链接到链表中。
3. P=P->next;：将指针 P 移动到下一个节点。现在 P 指向了新创建的节点，以便为它赋值。
4. P->data=i*2-1;：为当前节点的 data 成员赋值。这里应该是 P->data = i*2 - 1;，将当前节点的数据设为 i 乘以 2 减去 1 的结果。

所以，这个循环会创建四个新的节点，并在每个节点的 data 成员中存储一个奇数值（1、3、5、7）。

然后最后两行语句-----

• Ins_LinkList(L,i+1,i*2);：调用了一个名为 Ins_LinkList 的函数，将元素 i*2 插入到链表的第 i+1 个位置。
• Del_LinkList(L,i);：调用了一个名为 Del_LinkList 的函数，删除链表中的第 i 个元素(这里是不算头节点的,因为头节点没有被赋予元素?????)。

2.6

• while(P->next!=NULL) P=P->next;

这行代码是一个 while 循环，其目的是在链表中移动指针 P 直到 P 的下一个节点为 NULL，也就是链表的末尾节点。

解释如下：

1. P->next != NULL：这是一个条件表达式，它检查当前节点 P 的下一个节点是否不等于 NULL。条件表达式的结果是一个布尔值，如果当前节点的下一个节点不是 NULL，则条件为真，继续执行循环体。
2. P = P->next;：如果条件为真，就执行这行代码。这行代码将指针 P 移动到下一个节点，即将 P 更新为当前节点的下一个节点，以便继续检查下一个节点是否为链表的末尾。(终于理解😭)

循环将一直执行，直到 P 的下一个节点为 NULL，也就是链表的末尾节点。一旦链表末尾被找到，条件表达式为假，循环终止。这段代码通常用于遍历整个链表，直到到达链表的末尾节点。

总之，这段代码的目的是在链表中移动指针 P 直到达到链表的末尾节点。

已知 L 是带表头结点的非空单链表，和已知 L 是无表头结点的单链表，有什么区别

2.7

带表头结点和无表头结点的单链表在数据结构中有一些重要区别：

1. 存在与否：
   • 带表头结点的单链表： 这种链表在头部有一个额外的结点，通常称为表头结点或者哨兵结点。这个结点不存储实际的数据，它的主要目的是使链表操作更容易实现，因为它可以避免对空链表的特殊处理。带表头结点的链表通常在操作上更加统一，因为头结点始终存在，即使链表为空。
   • 无表头结点的单链表： 这种链表不包含表头结点，直接从第一个存储数据的结点开始。这意味着如果链表为空，那么链表头部就是一个空指针，需要特殊处理。
2. 索引/遍历起始点：
   • 带表头结点的单链表： 由于头结点的存在，链表的第一个数据结点从头结点的下一个结点开始，索引为1。
   • 无表头结点的单链表： 在没有头结点的情况下，链表的第一个数据结点通常是链表的头部，索引为0。
3. 空链表处理：
   • 带表头结点的单链表： 即使链表为空，头结点始终存在，因此对于空链表的处理与非空链表一样，不需要额外的特殊情况处理。
   • 无表头结点的单链表： 如果链表为空，头部就是一个空指针，需要特殊处理，否则在访问链表时可能会引发错误。
4. 操作实现的复杂性：
   • 带表头结点的单链表： 由于头结点的存在，通常可以更容易地实现插入和删除操作，因为不需要特殊情况处理头部节点。
   • 无表头结点的单链表： 操作实现可能稍微复杂一些，因为需要处理头部节点的特殊情况。

在实际应用中，选择使用带表头结点还是无表头结点的单链表取决于具体的需求和设计。带表头结点的链表通常在实现上更加统一和方便，而无表头结点的链表可能更节省一些内存空间。

首元结点&尾元结点

判断: 在带头结点的循环单链表中，尾元结点的next指针指向链表的首元结点。

false

尾元结点的next值指向链表的头节点，而不是首元结点。

首元结点指的是链表中存储第一个数据元素的结点。头节点是在首元结点之前设置的一个结点。

image-20230919200445761

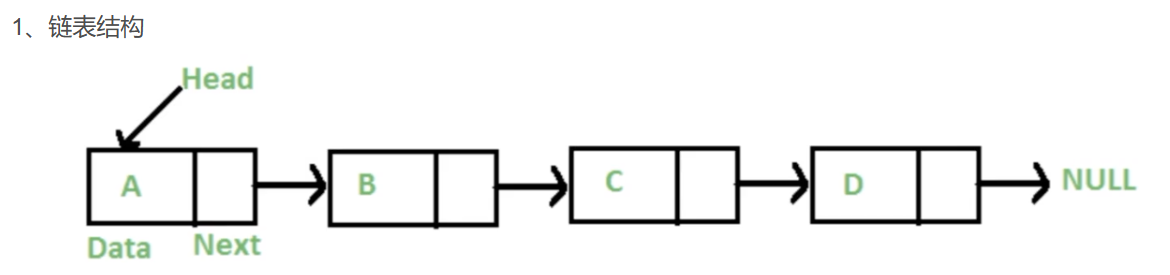
这里的D是尾元结点

【头结点】【头指针】【首元结点】

头结点（不一定有），存在为了方便操作，头结点是为了操作的统一和方便而设立的，放在第一个元素的结点之前，其数据域一般无意义（但也可以用来存放链表的长度），对在第一元素结点前插入结点和删除第一结点起操作与其它结点的操作就统一了。

首元结点：实际记录数据的第一个节点；

头指针：指向第一个物理节点地址的指针，就是定义的链表名，这个头指针的意义在于，在访问链表时，总要知道链表存储在什么位置（从何处开始访问），由于链表的特性（next指针），知道了头指针，那么整个链表的元素都能够被访问，也就是说头指针是必须存在的。

2.9

// 分析一下下面这段代码
Status A(LinkedList L) { //L 是无表头结点的单链表
if(L && L->next) {
    Q=L; L=L->next; P=L;
    while(P->next) P=P->next;
    P->next=Q; Q->next=NULL;
}
return OK;
}

这段代码是一个函数 Status A(LinkedList L)，其目的是将无表头结点的单链表 L 中的首元素移到链表的末尾。以下是代码的逐行解释：

1. if (L && L->next)：这是一个条件语句，确保链表 L 不为空且至少包含两个元素。如果链表为空或只包含一个元素，那么没有必要执行首元素移到末尾的操作。
2. Q = L;：创建一个指向链表头结点的指针 Q，用于暂时保存链表的首元素。
3. L = L->next;：将链表头指针 L 移动到链表的下一个元素，即跳过了原始的首元素。
4. P = L;：创建一个指向链表头结点的新指针 P，用于遍历链表并找到末尾元素。
5. while (P->next) P=P->next：进入一个循环，该循环将 P 移动到链表的最后一个元素，即当 P 的下一个元素不为空时继续执行。
6. P->next = Q;：将末尾元素的 next 指针指向原始首元素 Q，这样就将首元素移到了链表的末尾。
7. Q->next = NULL;：将原始首元素 Q 的 next 指针设置为 NULL，以确保它成为新链表的末尾元素。
8. return OK;：函数返回 OK，表示操作成功完成。

总之，这段代码的作用是将无表头结点的单链表 L 中的首元素移到链表的末尾。如果链表为空或只包含一个元素，则不执行任何操作。否则，它将通过重新连接指针来实现首元素的移动。

//分析一下下面这段代码
void BB(LNode *s, LNode *q) {
    // 声明指针 p，并将其初始化为 s
    p = s;
    // 当 p 指向的结点的下一个结点不等于 q 时，执行循环
    while (p->next != q) {
        // 将 p 移动到下一个结点
        p = p->next;
    }
    // 将 q 结点的 next 指针指向 s，形成闭环
    p->next = s;
}
void AA(LNode *pa, LNode *pb) {
    // 调用 BB 函数，将结点 pa 到 pb 之间的结点闭环
    BB(pa, pb);
    // 再次调用 BB 函数，将结点 pb 到 pa 之间的结点闭环
    BB(pb, pa);
}

2.11

• 2.11 设顺序表 va 中的数据元素递增有序。试写一算法，将 x 插入到顺序表的适当位置上，以保持该表的有序性。

Status InsertOrderList(SqList &va,ElemType x)
{
//在非递减的顺序表 va 中插入元素 x 并使其仍成为顺序表的算法
int i;
if(va.length==va.listsize)return(OVERFLOW);

for(i=va.length;i>0,x<va.elem[i-1];i--)
va.elem[i]=va.elem[i-1];

va.elem[i]=x;
va.length++;
return OK;

}

Status InsertOrderList(SqList &va,ElemType x)

这行代码是一个函数的声明，具体解释如下：

• Status：这是函数的返回类型。在C/C++中，函数通常会返回一个值，表示函数的执行结果或状态。在这里，函数返回类型是 Status，这意味着该函数会返回一个表示操作状态的值。
• InsertOrderList：这是函数的名称。函数名用于标识和调用函数。在这个情境下，函数名是 InsertOrderList，它表示这个函数的目的是将一个元素插入到一个顺序表中。
• (SqList &va, ElemType x)：这是函数的参数列表。它指定了函数接受的输入参数。具体解释如下：
  • SqList &va：这是第一个参数，它是一个引用（& 符号表示引用）。这意味着函数将接受一个名为 va 的参数，这个参数是一个 SqList 类型的顺序表。通过引用传递，函数可以直接修改传递给它的顺序表，而不需要复制整个数据结构，这可以提高性能并节省内存。
  • ElemType x：这是第二个参数，它是一个名为 x 的参数，表示要插入到顺序表中的元素。ElemType 可能是一个在代码的其他地方定义的数据类型，用于表示元素的类型。

综上，这行代码的含义是声明一个名为 InsertOrderList 的函数，该函数接受一个顺序表 va 和一个元素 x 作为参数，并且会返回一个 Status 类型的值，用于表示函数执行的状态或结果。

for (i = va.length; i > 0 && x < va.elem[i - 1]; i--) va.elem[i] = va.elem[i - 1];

• 这是一个 for 循环，从顺序表的最后一个元素开始向前遍历，同时检查元素 x 是否小于当前位置的元素。循环条件包括两部分：i > 0 表示循环要继续直到遍历到顺序表的第一个元素；x < va.elem[i - 1] 表示只要元素 x 小于当前位置的元素，就继续循环。这个循环的目的是找到插入位置。

• 在循环中，将当前位置的元素向后移动，以为新元素 x 腾出位置。这是为了为新元素 x 让路，为其找到适当的插入位置。

2.15

• 2.15 已知指针 ha 和 hb 分别指向两个单链表的头结点，并且已知两个链表的长度分别为 m 和 n。试写一算法将这两个链表连接在一起，假设指针 hc 指向连接后的链表的头结点，并要求算法以尽可能短的时间完成连接运算。

void MergeList_L(LinkList &ha,LinkList &hb,LinkList &hc) 
{ 
    LinkList pa,pb; 
    pa=ha; 
    pb=hb; 
    while(pa->next&&pb->next){ 
        pa=pa->next; 
        pb=pb->next; 
    } 
    if(!pa->next){          //pa到头了
        hc=hb; 
        while(pb->next) pb=pb->next; 
        pb->next=ha->next; 
    } 
    else{ 
        hc=ha; 
        while(pa->next) pa=pa->next; 
        pa->next=hb->next; 
    } 
}

2.16

已知指针 la 和 lb 分别指向两个无头结点单链表中的首元结点。写一个算法实现:

• 从表 la 中删除自第 i 个元素起共 len 个元素后，将它们插入到表 lb 中第 i 个元素之前。

2.22

• 试写一算法，对单链表实现就地逆置。

typedef struct Lnode {
    ElemType data; 
    struct Lnode *next; 
} Lnode, *LinkList;

//Lnode，将 struct Lnode 重命名为 Lnode，这允许我们在代码中使用 Lnode 来声明结构体类型的变量。？？
//LinkList，将 struct Lnode* 重命名为 LinkList，这样我们可以使用 LinkList 来声明指向链表节点的指针变量。

Status ListOppose_L(LinkList &L) 
{ 
    LinkList p,q;   //两个辅助指针
    p=L;       //将 p 指针指向链表头节点。
    p=p->next;  // 将 p 移动到链表的第一个真实节点，即跳过头节点。
    L->next=NULL; // 将头节点的 next 指针置空，即将逆置后的链表末尾节点的 next 指针指向空。
    while(p){ 
        q=p;         
        p=p->next;   //这两行就是把 q 指向 p，然后将 p 向后移动到下一个节点：
        q->next=L->next;  
        L->next=q;   //这两行就是进行插入，即：将 q 所指的节点插入到现在的表 L 的头结点和首元结点中间：
    } 
    return OK; 
}

试写一算法，对单链表进行逆置试写一算法,实现单链表的就地逆置(要求在原链表上进行)_白薇.的博客-CSDN博客

大佬！！！这篇博客解释的非常清楚

第三章

3.19

括号匹配

第六章 树

6.24

树转换成二叉树：

1. 加线，所有兄弟结点之间连接一条线；
2. 去线，对树中的每个结点，只保留它与第一个孩子结点的连线，删除与其他孩子结点之间的连线；
3. 层次调整，以树的根结点为轴心，将整个树调节一下（第一个孩子是结点的左孩子，兄弟转过来的孩子是结点的右孩子）；

1698111444872

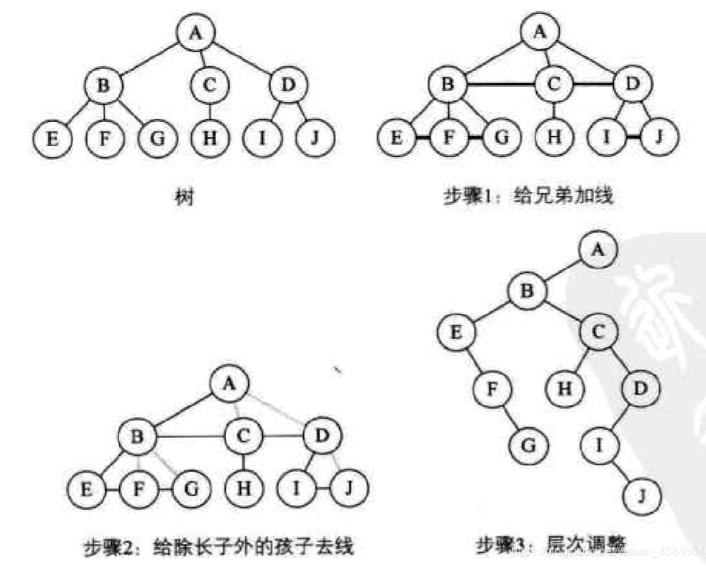
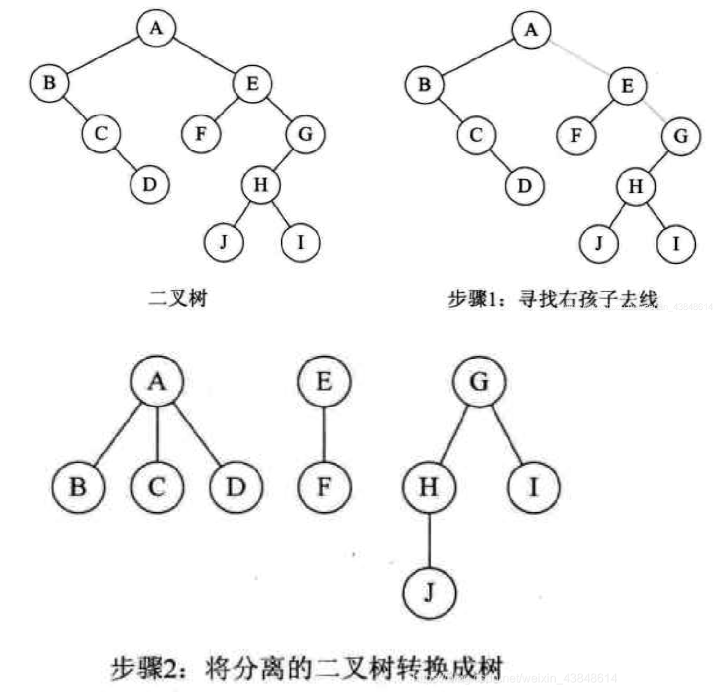
二叉树转换成树：

1. 加线。若某结点X的左孩子结点存在，则将这个左孩子的右孩子结点、右孩子的右孩子结点、右孩子的右孩子的右孩子结点…，都作为结点X的孩子。将结点X与这些右孩子结点用线连接起来。（即先将父节点与其所有非第一个孩子结点的结点相连）
2. 去线。删除原二叉树中所有结点与其右孩子结点的连线。
3. 层次调整。例子如下：

1698079388509

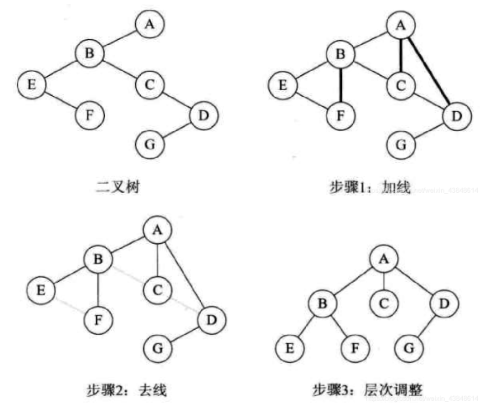
森林转换成二叉树：

森林是由若干棵树组成，可以将森林中的每棵树的根结点看作是兄弟，由于每棵树都可以转换为二叉树，所以森林也可以转换为二叉树。

1. 把每一棵树转换为二叉树
2. 第一棵二叉树不动，第二棵树开始，以此把后一棵二叉树的根结点作为前一棵树的根结点的右子树连接起来

1698112427431

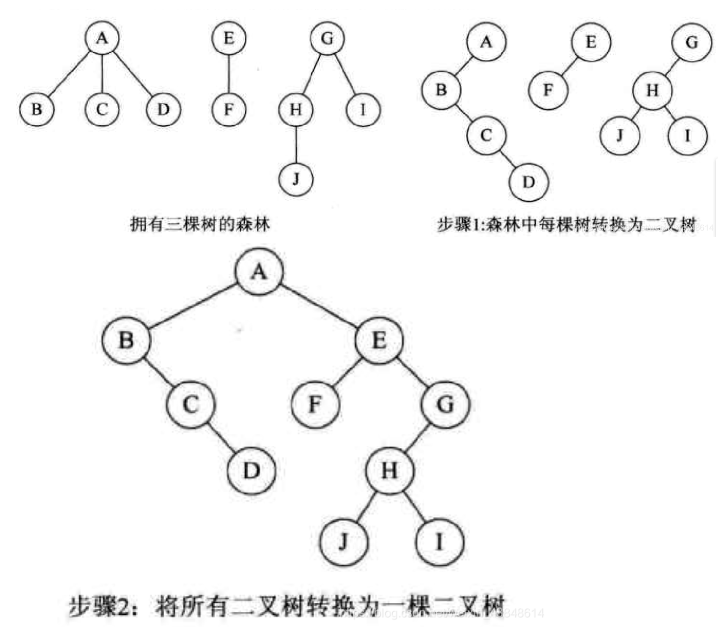
二叉树转换成森林：

• 看二叉树的根结点是否有右孩子，有右结点是森林，无右结点是树。（根据孩子兄弟表示法，一棵树的根结点转换为二叉树，其二叉树的根结点无右孩子）
• 若是森林：
  • 依次把与右孩子结点的连线删除，得到分离的二叉树
  • 把分离后的每棵二叉树转换为树；
  • 整理第（2）步得到的树，使之规范，这样得到森林。例子如下：

  • 

    1698079139900

• 若是树：
  • 参照二叉树转换成树