通信原理与安全技术概述

本文最后更新于：2023年12月1日 下午

大三上选的一门选修课——《通信原理与安全》的部分笔记

第一章 绪论

1.1 通信的基本概念

通信（Communication）——沟通信息。

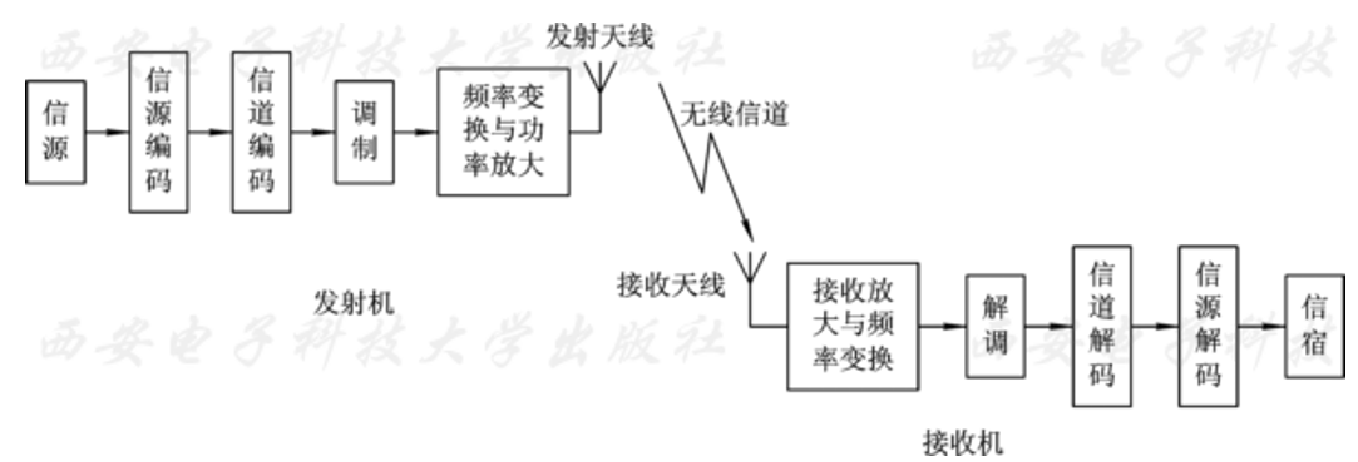
通信系统——发送器、信道、接收器。

信源（发信者）：把各种消息转换成原始电信号。该信号含有丰富的低频成分甚至直流分量，因此又称基带信号。

信道：信号传输的通道。

信宿（收信者）：将复原的原始电信号转换成相应的消息。

噪声源：噪声源不是人为加入的设备，而是通信系统中各种设备以及信道中所固有的，并且是人们所不希望的。

image-20231117141146493

知识是一种具有普遍和概括性质的高层次信息

消息是信息的载体，而不是信息本身

消息变换成适合信道传输的物理量（电磁波、光），就是信号。

1949年，香农在Bell System Technical Journal上发表了著名论文《通信的数学原理》（ A mathematical theory of communication ）以及《噪声下的通信》（ Communication in the presence of noise ），对信息作出定义，并阐明了通信的基本问题，给出了通信系统的模型，提出了信息量的数学表达式，并探讨了信道容量，信源编码，信道编码等一系列基本问题，是通信的奠基性著作。

香农对信息的定义

香农给出定义：信息是对事物运动状态或存在方式的不确定性的描述

首先，香农注意到消息的信息量与消息本身的不确定性有关。例如，抛一枚硬币，如果正面出现的概率是99%，那么当我们得知抛掷的结果是反面时得到的信息量会比得知是正面时得到的信息量大。

其次，他发现通信的目的就是要消除不确定性。具体地讲，信息传递过程是一个从不知到知的过程（理想信道）或者是一个从知之甚少到知之甚多的过程（有噪信道）

1.2 几个数学概念

image-20231117141604674

单个消息信息量的数学定义

image-20231117141746926

信息量的单位：

  • a = 2，则为比特（bit），最常用
  • a = e，则为奈特（nat）

信息源信息量的数学定义：熵

image-20231117142925095

1.3 现代通信的发展

按照通信方式：

  • 原始通信：烽火、驿站、邮政
  • 有线通信：计算机网络，有线电话，光纤通信
  • 无线通信 (本课程的重点)：蜂窝网（移动通信）、WIFI、蓝牙等

按照信号类型：

  • 模拟通信：系统传输模拟信号
  • 数字通信：系统传输数字信号

#### 无线通信的发展史

移动通信（蜂窝网）

  • 第一代（1G）：模拟通信（大哥大）
  • 第二代（2G）：GSM（FDMA频分多址），数字通信的开始
  • 第三代（3G）：CDMA2000（电信），WCDMA（联通），TD-SCDMA（移动，我国自主研发）
  • 第四代（4G）：LTE （TD-LTE，FD-LTE），OFDM+MIMO
  • 第五代（5G）：NR (New Radio)，三大场景：增强的移动宽带，海量接入，超可靠低时延（eMBB, mMTC, URLLC）
  • 第六代（6G）：正在理论探讨阶段

局域网：WLAN (WiFi)

蓝牙、ZigBee

无线通信系统的基本构成

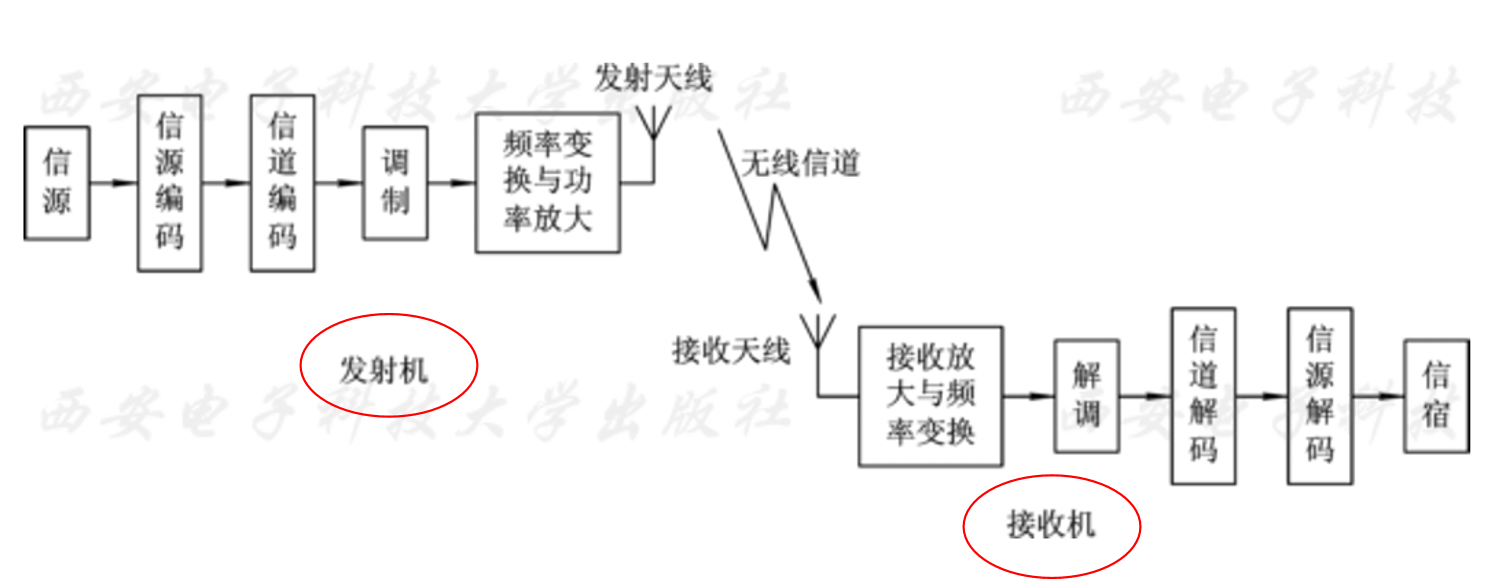
image-20231117144535016

无线通信系统的性能指标

  • 有效性---速度指标

  • 可靠性---质量指标，与有效性相矛盾

  • 安全性

无线通信安全简史

移动通信方面

第一代：几乎没有安全措施，用户（手机）把自己的序列号发送至网络（例如基站），网络查一下有这个序列号就允许其连接，一旦手机序列号被克隆，别人就可以使用相应的网络服务

第二代（GSM）：

特点：

  • 采用基于私钥密码体制的安全机制

  • 通过鉴权（认证）来防止非法用户使用网络

  • 通过加密技术防止无线信道的窃听

缺点：

  • 所使用的身份认证和加密算法存在许多安全隐患
  • 安全密钥太短可能被短时间破译
  • SIM卡可能被克隆
  • 没有考虑数据完整性保护，难以发现数据被篡改

3G, 4G, 5G：

特点：

  • 重新设计安全算法

  • 增加密钥长度

  • 提供双向认证（用户与网络）

  • 保证数据的完整性

  • 安全体系趋于稳定

挑战：超级计算机，密钥分发和管理

WLAN：非商用，不盈利，所以研究人员只关注速率、时延等性能，安全性考虑较少，目前常用的是RC4和AES算法

无线通信网面临的主要安全威胁

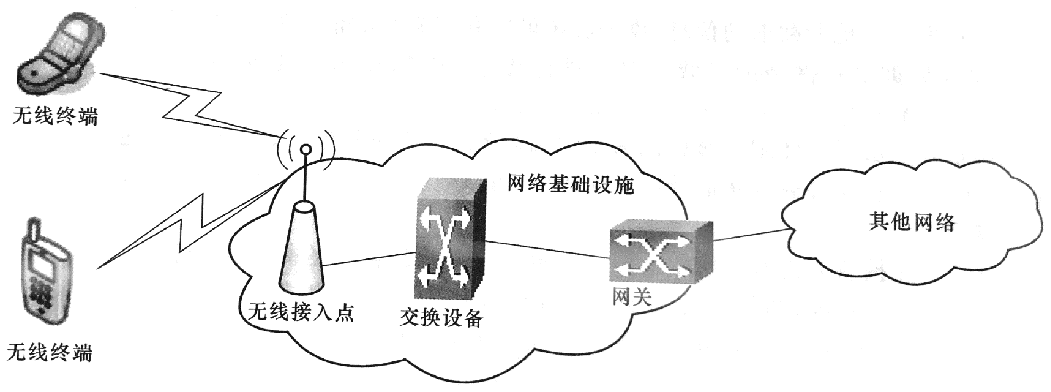
image-20231117150033846

首先来明确几个概念

  • 无线终端：手机，pad，笔记本电脑等
  • 无线接入点：小基站、路由器等
  • 网络基础设施：大基站，交换机
  • 空中接口：无线终端与无线接入点之间的接口

移动通信系统面临的威胁可以分成三大类

  • 对传递信息的威胁：这类威胁针对系统中传输的个人信息（语音、短信等）
  • 对用户的威胁：这类威胁针对用户的行为（用户在哪，在做什么等）
  • 对通信系统的威胁破坏系统的完整，访问权限等

对传递信息的威胁

  • 侦听

    • 可以理解为非法窃听

    • 无线通信的广播特性使得任何具有天线的设备都能收到其他用户的数据

  • 篡改：非授权方更改系统中的各种信息，伪装成合法用户进行信息的修改

  • 抵赖：通信一方否认自己的行为

对用户的威胁

  • 流量分析：分析信息速率，消息长度，接收者或者发送者标识等
  • 监视：了解用户在何时何地进行通信

对通信系统的威胁

  • 拒绝服务
    • 非法攻击使系统无法提供服务
    • 例如发送大量垃圾信息造成网络拥堵，阻止系统对正常用户的服务
  • 资源的非授权访问
    • 越权使用超过其职权范围的资源
    • 例如学信网学生注册信息丢失
    • 强行占用不属于自己的信道

移动通信系统的安全要求

1）能唯一地标识用户

2）冒充合法用户是困难的

3）双向认证。用户和服务器之间相互信任

4）机密性。保证传输数据的安全

5）用户身份的匿名性。不向第三方暴露自己的身份

6）不可否认性。防止抵赖

7）完整性

1.4 专有名词缩略表

1
2
3
4
5
6
7
8
GSM：Global system for mobile communications
W-CDMA: wideband-code division multiple access
TD-SCDMA: time division-synchronous code division multiple access
LTE: long term evolusion
NR: new radio
eMBB: Enhanced Mobile Broadband
mMTC: Massive Machine Type Communication
URLLC: Ultra Reliable Low Latency Communication

第二章 信源编码

2.1 采样定理

信源有两种，离散源和模拟源（连续源）

1、为了使数字电路能够处理模拟信号，必须将模拟信号转成数字信号。将模拟信号到数字信号的转换称为模-数转换（A/D）。实现A/D的电路称为ADC。

2、模拟信号与数字信号之间的桥梁是什么呢？什么时候它们可以相互转换呢？

--- 回忆一下你在地铁里见到的广告牌？啥意思？我也没看懂😮😮

--- 回忆一下你在纸上按照“点”描摹一条曲线

采样定理：\(f_s≥2f_{amax}\)

\(f_s\)为采样频率， \(f_{amax}\)为奈奎斯特频率，它是模拟信号中的最高频率成分(谐波)

image-20231117153211124

2.2 量化和编码

通过采样后，我们得到了一个离散的数值。因为得到的数值有可能有无穷多位的小数，所以总是要进行近似，这个近似的过程就称为量化

量化：将采样的数值用一个最小单元的整数倍来表示。这个最小单元记为Δ

编码：将量化后的数值用二进制代码表示的过程。

量化误差：在量化过程中（数值近似），不可避免地会引入误差。不同的量化方法引入的量化误差不同。

2.3 信源编码

编码？说白了就是取名字（给信号或消息等取名字）

将一号给予班长，二号给予学委，三号….对A,B两个字母编码，可分别为0,1….

举例

某事件有四种可能，你会如何对这四种情况进行编码？ \[ \begin{array}{|l|l|} \hline X & P(x) \\ \hline \text { a } & 0.6 \\ \hline \text { b } & 0.39 \\ \hline \text { c } & 0.009 \\ \hline \text { d } & 0.001 \\ \hline \end{array} \]

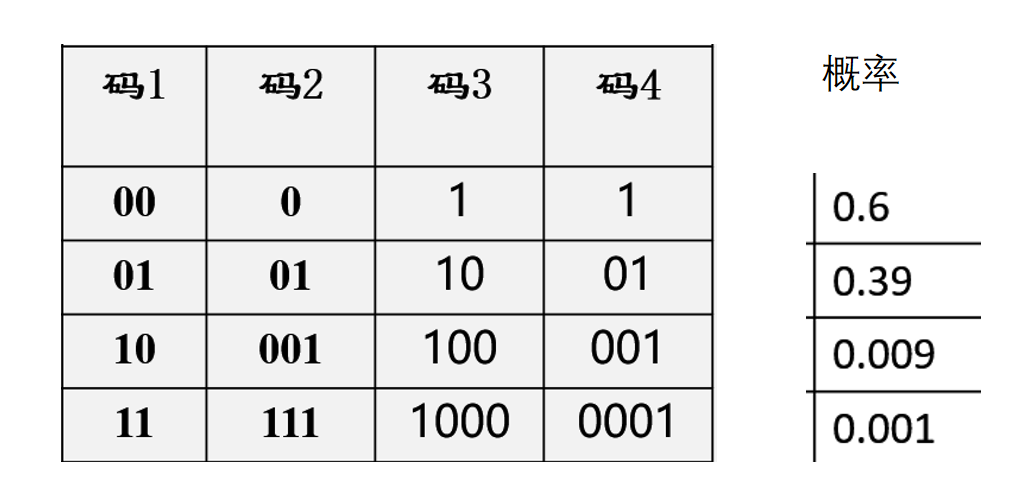
image-20231117164758584

码1是否可行？ 可行

码2是否可行？0010，译码是否唯一？不可行

码3是否可行？ 可行，但是当我们收到一串码符号10时，我们能否判断该码字是否传完？ 所以还是不建议这样

码4是否可行？

  • 当收到一串码符号01时，能否判断该码字是否传完？出现00，能否判断？
  • 第一问答案是肯定的。因为只要出现1，对应的码字就结束了。第二问的答案也是肯定的。没有出现1，则该码字还没有传完。
  • 码4在译码时无需依赖于后续的码符号就可以判断该码字有没传完。这种类型的码就是即时码。

对所选编码的要求：

  • 唯一可译性（必须满足）
  • 即时性（尽量满足）

目前满足以上两个要求的码有码1和码4，请问实际中你会选哪一种，为什么？

计算码1的平均长度，答案：2

计算码4的平均长度，答案：1×0.6 + 2×0.39 + 3×0.009 + 4×0.001 = 1.411 < 2

以上例子告诉我们一个什么道理？概率越大，码元编码越短，则信源的平均编码长度越短

这就是数据压缩的原理！

Huffman码(哈夫曼编码)

霍夫曼码的定义
例题1
解决方案1

\(\overline L\)为平均长度

解决方案2
两种方案的对比

所以我们总是用第二种方法来进行哈夫曼编码

Huffman码的特点：

1、 Huffman码是最佳码（在所有码中平均码长最小）

2、概率大的符号对应于短码，概率小的符号对应于长码

3、两个概率最小的码字具有相同的码长，且只有最后一位不同

2.4 小结

本章小结

第三章 无线信道

  • 一条水管能输送多少自来水？

  • 一条高压线能传输多少电？

学完本章，我们能够回答一个问题：无线信道究竟能传输多少信息？

3.1 无线信道模型

无线信道是该课程接下来所有内容的基础

无线信道最主要的特征：随时间、频率而发生强度和相位的变化

无线信道的变化可以粗略地分为两大类：大尺度衰落、小尺度衰落

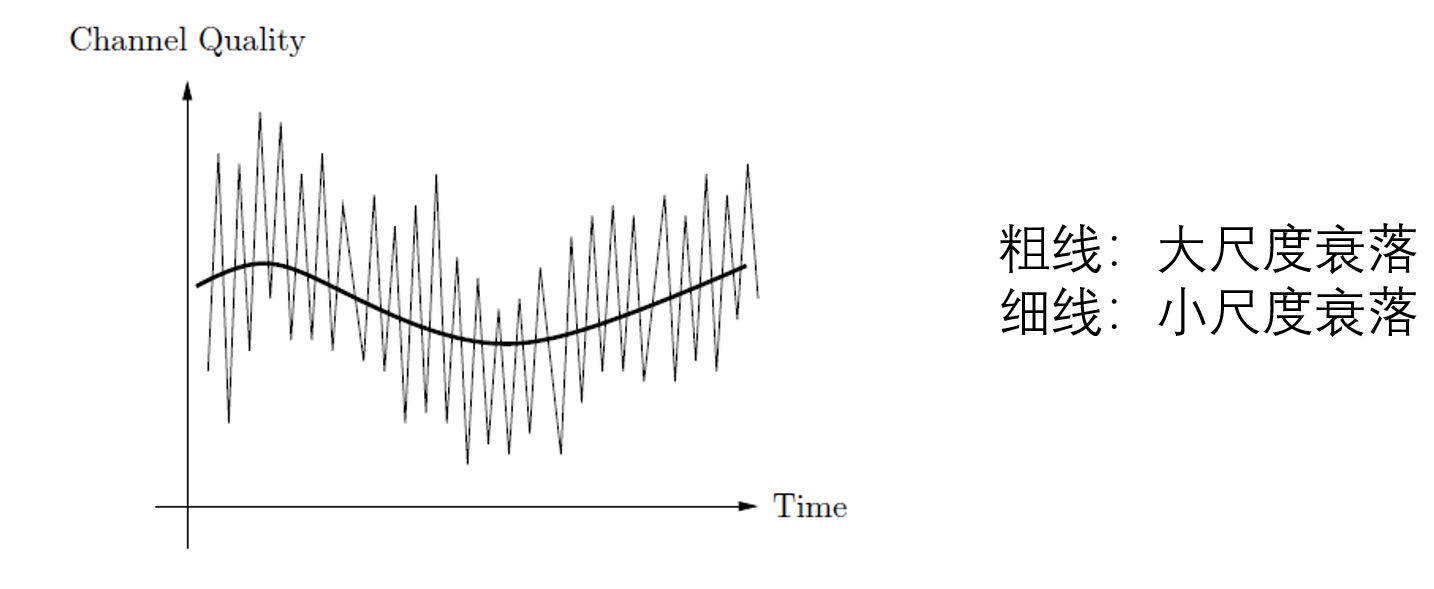
无线信道的变化

大尺度衰落一般与路径损耗以及阴影有关，变化幅度较小，实际中主要影响的是基站的位置

小尺度衰落一般由多径和干扰引起，变化幅度剧烈，实际中主要影响传输的可靠性和有效性，是本课程研究的重点

第四章 信道编码

无线通信系统的基本构成

4.1 香农定理

有噪信道编码定理（香农第二定理）

某一信道的信道容量为C。当信息传输速率\(R≤C\)时，总能找到一种信道编码方法，使信道输出端的平均译码错误概率任意小。

结论：信道容量是在信道中可靠传输信息的最大信息传输速率。

问题：香农第二定理只告诉我们存在一种编码方式使错误概率趋于零，但却没有告诉我们这种编码具体是什么？当传输速率小于C时，采用什么方式进行编码可以实现香农第二定理呢？

答：信道纠错码

4.2 纠错码

基本概念1：

有\(k\)个信息，记为\(m=(m_{k-1},m_{k-2},…,m_0)\)。称m为信息组，\(m_i\)为信息元

这k个信息元一共有\(2^k\)种组合方式（二元通信系统）

为了纠错，在\(k\)个信息的基础上引入额外的\(r\)个符号（称为校验元），形成 \(n=k+r\) 长的序列，并记为\(C=(c_{n-1},c_{n-2},…,c_0)\)，称\(C\)为码字， \(c_i\)为码元，\(n\)是码长，\(k\)是信息元的个数，\(n-k=r\)是校验元的个数

  • 如果增加的\(r\)个校验元只与本组的\(k\)个信息元有关，而与其他信息组无关，则这样的码称为分组码，记为(n,k)码。

  • 如果增加的\(r\)个校验元不仅与本组的\(k\)个信息元有关，还与之前的信息组有关，则这样的码称为卷积码。

  • 对二进制\((n, k)\)线性分组码\(C\) ，\(k\)个信息元对应产生 \(2^k\)个许用码字，其他\(2^n- 2^k\)个为禁用码字。

基本概念2：码字的汉明重量、汉明距离

码字的汉明重量是指码字中非零码元的个数，记为\(W(C)\)。对于二元码，汉明重量就是\(1\)的个数。

因此, 两个码字 \(C_k\) 和 \(C_j\) 之间的汉明距离为 \[ D\left(C_k, C_j\right)=W\left(C_k \oplus C_j\right) \] \(\oplus\) 表示模二相加, 或者异或

\[ \begin{array}{r} \text {1101与1010之间的汉明距离: } \\ 1101 \\ +1010 \\ \hline 0111 \end{array} \]

基本概念3：错误图样 \[ E=\left(e_{n-1} e_{n-2} \cdots e_0\right) \]

当 \(e_i=0\) 时，表示第 \(\mathrm{i}\) 位无差错发生； \(e_i=1\) 时，表示第 \(\mathrm{i}\) 位出错

假设传输的序列为 \(C\), 接收的序列为 \(R\), 则 \[ E=C \oplus R \quad R=C \oplus E \quad C=R \oplus E \]

即，任意两个的模二和等于第三个

\(W(E)\) 就表示出现错误的个数。

发送1101，接收1010，判断哪些位出错：后三位都有错误

4.3 线性分组码

定义：线性分组码是指分组码中信息元和校验元是用线性方程联系起来的一种差错控制码

线性分组码的构成步骤：

1、信道编码器将信息序列分成 \(k\) 长的信息组, 记为 \(\mathrm{m}=\left(\mathrm{m}_{\mathrm{k}-1}, \mathrm{~m}_{\mathrm{k}-2}, \ldots, \mathrm{m}_0\right)\) 。

2、用 \(\mathrm{k}\) 个信息元线性组合产生 \(\mathrm{r}\) 个校验元

3、将 \(k\) 个信息元与 \(\mathrm{r}\) 个校验元组合成长度为 \(n\) 的码字 \(\mathrm{C}=\left(\mathrm{c}_{\mathrm{n}-1}, \mathrm{c}_{\mathrm{n}-2}, \ldots, \mathrm{c}_0\right)\)

线性分组码

4.4 汉明码

最简单的线性分组码：汉明码

汉明码可以用来纠正 1 比特错误

汉明码的核心在于两个矩阵：生成矩阵G和校验矩阵H

  • 生成矩阵G用来生成码字
  • 校验矩阵H用来验证某个码字是否传输正确

一、生成矩阵

（用来生成码字）

生成矩阵
生成矩阵
生成矩阵

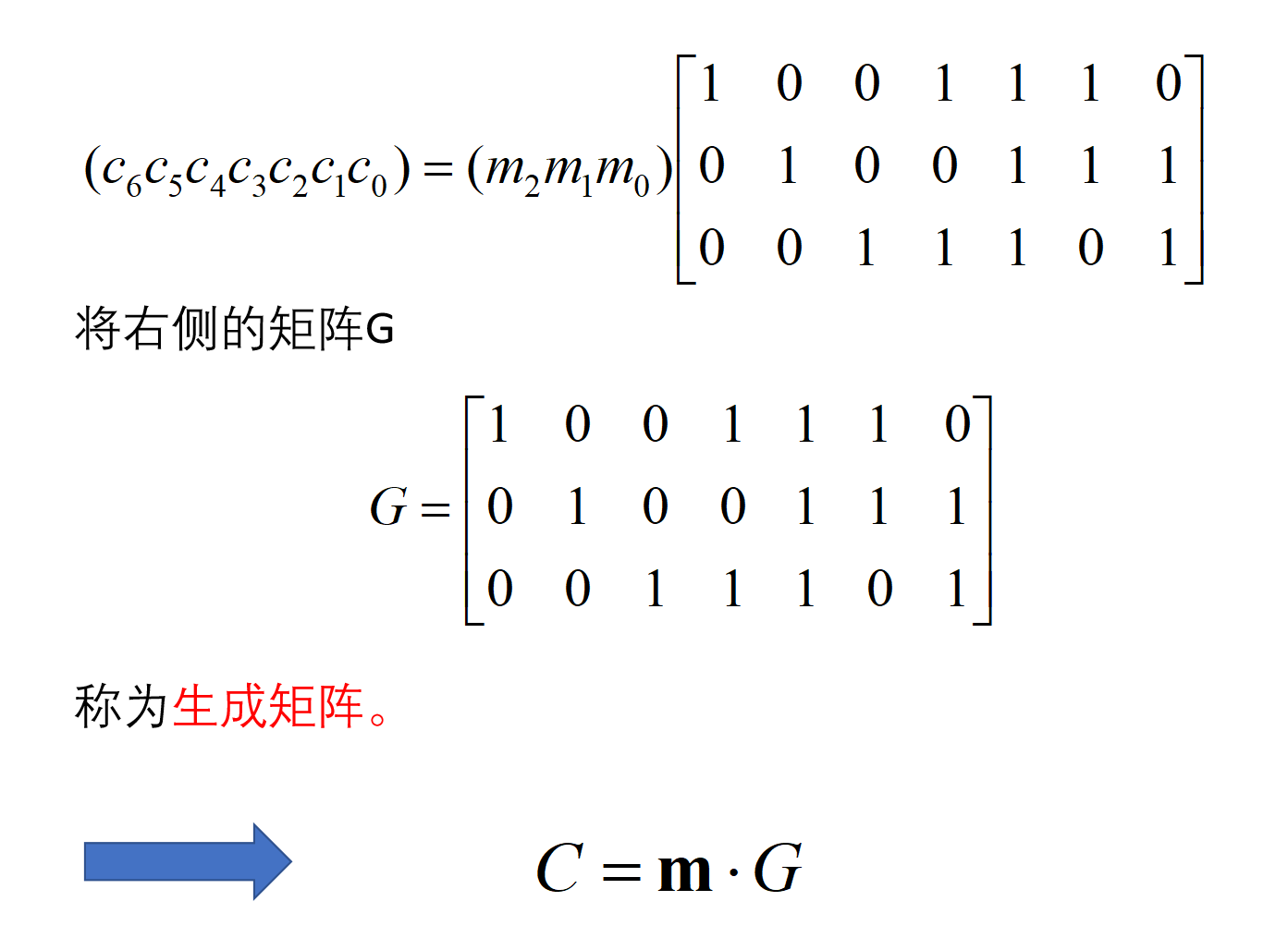
下面是信息论与编码中的一点东西

（7，4）汉明码的标准校验矩阵

\[ \begin{aligned} &\begin{array}{|l|l|l|l|l|l|l|l|l|} \hline s 0=000 & \mathrm{c} 0=0000000 & \mathrm{c} 1=0001011 & \mathrm{c} 2=0010110 & \mathrm{c} 3=0011101 & \mathrm{c} 4=0100111 & \mathrm{c5}=0101100 & \mathrm{c} 6=0110001 & \mathrm{c} 7=0111010 \\ \hline \mathrm{s} 1=101 & \mathrm{e} 1=1000000 & 1001011 & 1010110 & 1011101 & 1100111 & 1101100 & 1110001 & 1111010 \\ \mathrm{~s} 2=111 & \mathrm{e} 2=0100000 & 0101011 & 0110110 & 0111101 & 0000111 & 0001100 & 0010001 & 0011010 \\ \mathrm{~s} 3=110 & \mathrm{e} 3=0010000 & 0011011 & 0000110 & 0001101 & 0110111 & 0111100 & 0100001 & 0101010 \\ \mathrm{~s} 4=011 & \mathrm{e} 4=0001000 & 0000011 & 0011110 & 0010101 & 0101111 & 0100100 & 0111001 & 0110010 \\ \mathrm{~s} 5=100 & \mathrm{e} 5=0000100 & 0001111 & 0010010 & 0011001 & 0100011 & 0101000 & 0110101 & 011110 \\ \mathrm{~s} 6=010 & \mathrm{e} 6=0000010 & 0001001 & 0010100 & 0011111 & 0100101 & 0101110 & 0110011 & 0111000 \\ \mathrm{~s} 7=001 & \mathrm{e} 7=0000001 & 0001010 & 0010110 & 0011100 & 0100110 & 0101101 & 0110000 & 0111011 \\ \hline \end{array}\\ &\begin{array}{|l|l|l|l|l|l|l|l|l|} \hline s 0=000 & c 8=1000101 & c 9=1001110 & c 10=1010011 & c 11=1011000 & c 12=1100010 & c 13=1101001 & c 14=1110100 & c 15=1111111 \\ \hline s 1=101 & 0000101 & 0001110 & 0010011 & 0011000 & 0100010 & 0101001 & 0110100 & 0111111 \\ s 2=111 & 1100101 & 1101110 & 1110011 & 1111000 & 1000010 & 1001001 & 1010100 & 1011111 \\ s 3=110 & 1010101 & 1011110 & 1000011 & 1001000 & 1110010 & 1111001 & 1100100 & 1101111 \\ s 4=011 & 1001101 & 1000110 & 1011011 & 1010000 & 1101010 & 1100001 & 1111100 & 1110111 \\ s 5=100 & 1000001 & 1001010 & 1010111 & 1011100 & 1100110 & 1101101 & 1110000 & 1111011 \\ s 6=010 & 1000111 & 1001100 & 1010001 & 1011010 & 1100000 & 1101011 & 1110110 & 1111101 \\ s 7=001 & 1000100 & 1001111 & 1010010 & 1011001 & 1100011 & 1101000 & 1110101 & 1111110 \\ \hline \end{array} \end{aligned} \]

……

……

……

……

第十章 无线通信安全

通信：

有线：光纤

无线：

  • 光通信
  • 分子通信——药物
  • 量子通信

安全性原则

假设A要通过信封向B邮寄一个100元的支票。通常，A和B会考虑什么因素？

A要保证只有B能收到信封，即使别人收到，也不知道支票的细节。这是保密性原则

A和B还要保证别人不会篡改支票内容（如金额、日期、签名、收款人等）。这是完整性原则

B要保证支票是来自A，而不是别人假装A（否则就是假支票）。这是认证原则。

如果B把支票转入账号中，钱从A账户转到B账户之后，A否认签发了支票呢？法院要用A的签名否认A的抵赖，解决争端。这是不可抵赖性原则。

保密性

保密性要求做到只有发送人和期望接收人才能访问消息内容。如果非法人员能够访问消息内容，则破坏了保密性原则。

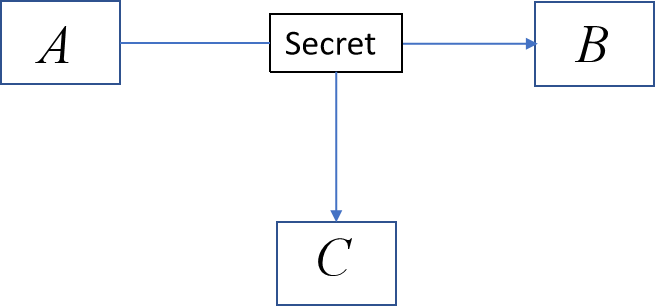
image-20231117142405434

例如该图中，A向B发送一封邮件，C未经B的允许却可以进行访问。这种攻击称为截获（Interception）

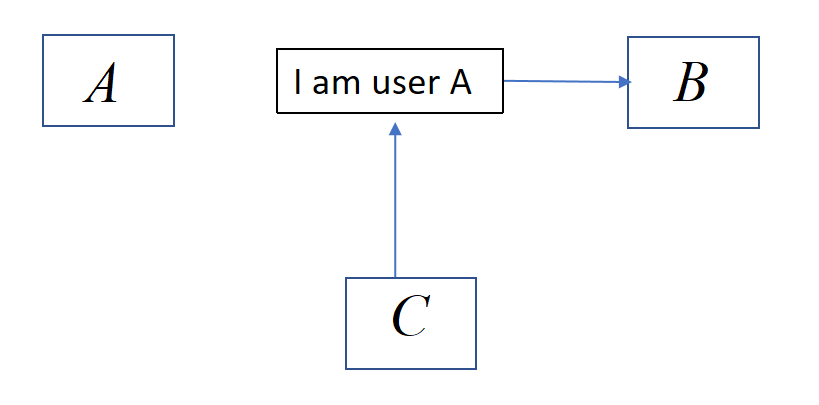
认证

认证机制用于证明身份。例如，用户C假装成用户A向B发送转账请求（实际收款账户是C的而不是A的），B以为这是A的请求，于是错误地将钱打给C。这种攻击称为伪造(fabrication)

image-20231117142504430

完整性

消息内容在发送方发出后到达期望接收方时发生改变，就会失去消息的完整性。

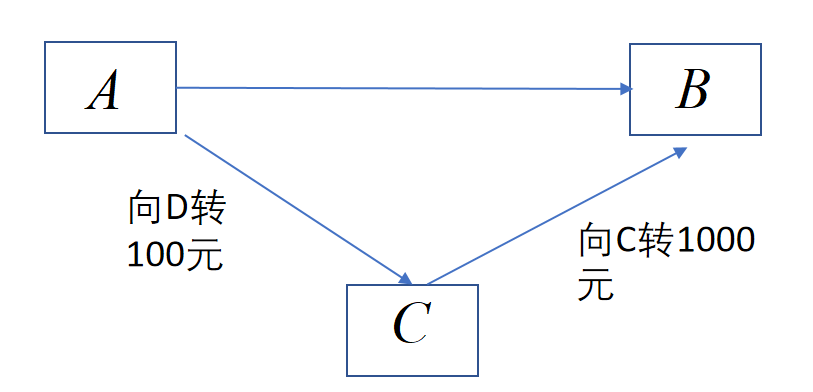
image-20231117142530983

C篡改了A发送的信息，然后将改变的信息发给B。A，B都不知道消息被篡改。这种攻击称为篡改(modification)

不可抵赖

有时用户发送了这个消息，又想否认发送了这个消息。

image-20231117142604861

例如，用户A向银行B发送一个转账请求。银行按A的请求转账之后，A声称没有发送这个转账请求

无线通信的开放性

无线信道的开放性导致任何装有天线的用户都可以收到发送给其他用户的信息

这种特性被称为广播特性，例如，上课、讲座等

信息论安全（完美安全）

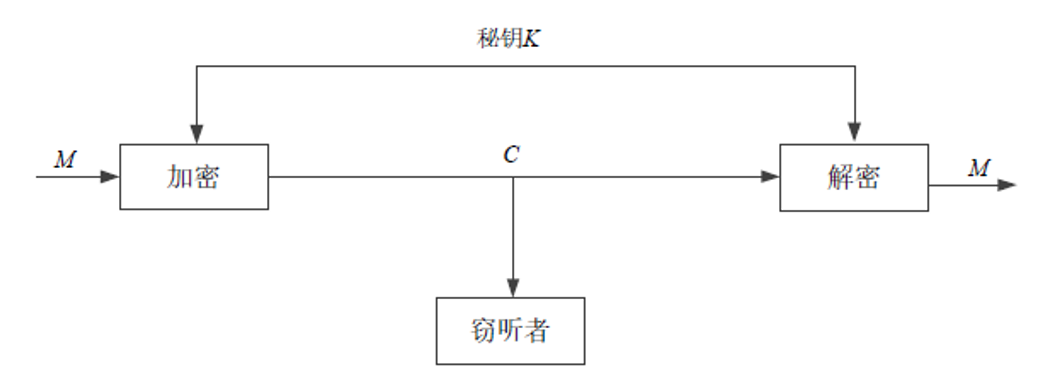
image-20231117142757724

M是隐私信息（明文），K是密钥，C是M被K加密后的信息（密文）

香农证明：要实现完美安全，M与C必须满足如下关系：

\[ I(M;C)=0 ---互信息 \]

意味着窃听者收到C后得到关于M的信息量为0；又或者理解为M与C没有任何共有的信息。

加密的性质：知道了M，K，C 中的任何两个，第三个就会知道，因此：\(H(M|KC) = H(K|MC) = H(C|KM)=0\)

完美安全的条件：一次一密，即每一比特的隐私信息至少需要一比特的密钥进行加密

互信息

image-20231117143815037

熵 H(X)：熵的本质是不确定性的多少

条件熵 H(X|Y)：已知Y后，X还剩下多少不确定性 \[ H(X \mid Y)=-\sum_i \sum_j P\left(x_i, y_j\right) \log P\left(x_j \mid y_i\right) \] 在没有收到Y时，X的不确定性为多少？ H(X)

在收到Y后，X的不确定性为多少？H(X|Y) 。这个对 X 尚存在的不确定性是由干扰（噪声）引起的。

在这个过程中，接收机获得了多少信息量？H(X)-H(X|Y)

互信息： \[ I(X;Y)=H(X)-H(X|Y) \] 互信息I(X;Y)的本质：接收机获取来自发射机的信息量的多少。或者理解为：接收信号Y与发送信号X共有的信息量

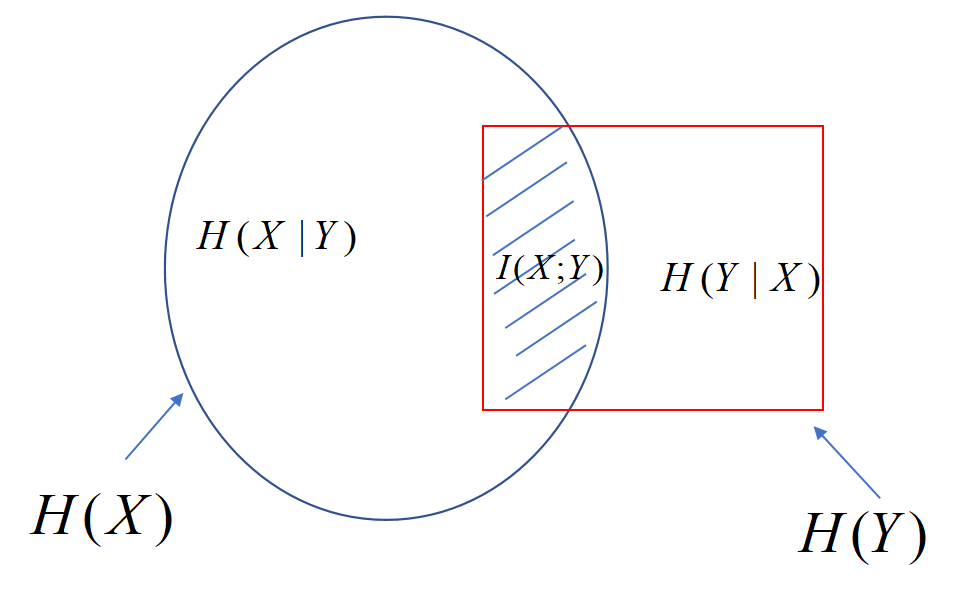
image-20231117144412928

H(X|Y)：去掉包含Y的部分后，X剩下的不确定性

H(Y|X)：去掉包含X的部分后，Y剩下的不确定性

如果发送了X，接收机准确地获取了X，则得到的互信息为多少？H(X)

如果发送了X，收到了一个完全不相干的Y，则得到的互信息为多少？0

Diffie-Hellman密钥交换协议

1976年， Diffie和Hellman这两个人提出了一种奇妙的密钥交换方法来解决通信双方密钥共享的问题。该方案是后续非对称密码学的基础

算法描述：

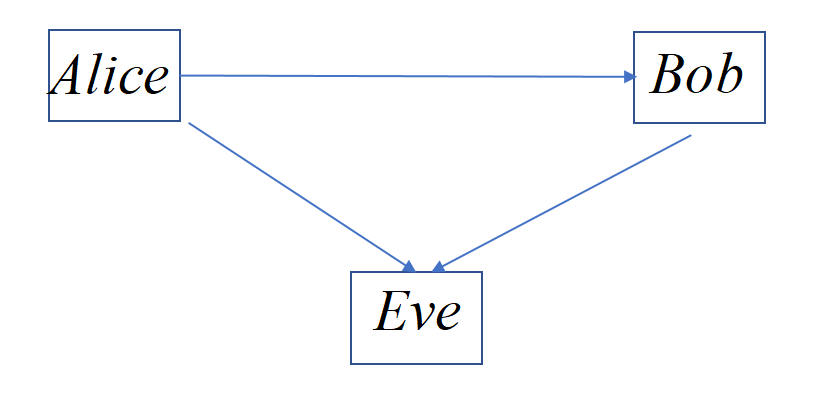
image-20231117151709336

第一步：Alice和Bob公开两个大的素数n,g。意味着Alice，Bob，Eve都知道这两个数

第二步：Alice生成一个很大的数x（只有Alice自己知道），并计算\(A=g^x \bmod n\)

第三步：将A发送给Bob（意味着Bob，Eve都知道A）

第四步：Bob生成一个很大的数y（只有Bob自己知道），并计算\(B=g^y \bmod n\)

第五步：将B发送给Alice（意味着Alice，Eve都知道B）

第六步：Alice计算秘密密钥K1；Bob计算秘密密钥K2

\[ \begin{align} &K_1=B^x \bmod n----B是来自Bob，x是Alice生成\\ &K_2=A^y \bmod n----A是来自Alice，y是Bob生成\\ \end{align} \]

证明1：K1=K2 \[ \begin{aligned} & K 1=B^x \bmod n \\ & \because B=g^y \bmod n \\ & \therefore g^y=r n+B(r \text { 是一个整数 }) \\ & \therefore\left(g^y\right)^x \bmod n=(r n+B)^x \bmod n=B^x \bmod n=K 1 \\ & K 1=g^{y x} \bmod n \\ & K 2=g^{x y} \bmod n \\ & K 1=K 2=K\end{aligned} \] 证明2：Eve很难算出K

Eve要解出K，必须知道x或者y，\(K_1=B^x \bmod n\)，\(K_2=A^y \bmod n\)

而要算出x和y只能从以下两个方程入手：\(A=g^x \bmod n\)，\(B=g^y \bmod n\)

因为x,y是整数且n很大，从这两个方程求出x和y非常困难

看个小例子：\(2=3^y \bmod 17\)，遍历得\(x=14\)

#通信原理与安全
通信原理与安全技术概述
http://viper2383.github.io/2023/11/17/通信原理与安全技术概述/
作者
w1per3
发布于
2023年11月17日
许可协议