数据结构 排序

下面这个网站动态的演示了各种排序算法，可以更加直观的了解一下

排序（冒泡排序，选择排序，插入排序，归并排序，快速排序，计数排序，基数排序） - VisuAlgo

十个经典排序算法

排序算法可以分为内部排序和外部排序，内部排序是数据记录在内存中进行排序，而外部排序是因排序的数据很大，一次不能容纳全部的排序记录，在排序过程中需要访问外存。

排序算法总结

名词解释：

n：数据规模

k：“桶”的个数

In-place：占用常数内存，不占用额外内存

Out-place：占用额外内存

排序算法稳定性：

假定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记录的相对次序保持不变，即在原序列中，r[i]=r[j]，且r[i]在r[j]之前，而在排序后的序列中，r[i]仍在r[j]之前，则称这种排序算法是稳定的；否则称为不稳定的。

对于不稳定的排序算法，只要举出一个实例，即可说明它的不稳定性；而对于稳定的排序算法，必须对算法进行分析从而得到稳定的特性。需要注意的是，排序算法是否为稳定的是由具体算法决定的，不稳定的算法在某种条件下可以变为稳定的算法，而稳定的算法在某种条件下也可以变为不稳定的算法。

• 时间复杂度： 一个算法执行所耗费的时间。
• 空间复杂度：运行完一个程序所需内存的大小（辅助空间）。

关于稳定性：

稳定的排序算法：冒泡排序、插入排序、归并排序和基数排序。

不是稳定的排序算法：选择排序、快速排序、希尔排序、堆排序。

选择排序分类

• 简单选择排序

• 树型选择排序

• 堆排序

简单选择排序

算法思想

对于具有 n 个记录的无序表遍历 n-1 次，第 i 次从无序表中第 i 个记录开始，找出后序关键字中最小的记录，然后放置在第 i 的位置上。

简单选择排序动图演示

算法代码

堆排序

堆の概念

首先要了解一下堆的含义：在含有 n 个元素的序列中，如果序列中的元素满足下面其中一种关系时，此序列可以称之为堆。

• \(k_i ≤ k_{2i}\)且 \(k_i ≤ k_{2i+1}\)（在 n 个记录的范围内，第 \(i\) 个关键字的值小于第 \(2i\) 个关键字，同时也小于第 \(2i+1\) 个关键字）
• \(k_i ≥ k_{2i}\)且 \(k_i ≥ k_{2i+1}\)（在 n 个记录的范围内，第 \(i\) 个关键字的值大于第 \(2i\) 个关键字，同时也大于第 \(2i+1\) 个关键字）

对于堆的定义也可以使用完全二叉树来解释，因为在完全二叉树中第 i 个结点的左孩子恰好是第 2i 个结点，右孩子恰好是 2i+1 个结点

如果该序列可以被称为堆，则使用该序列构建的完全二叉树中，每个根结点的值都必须不小于（或者不大于）左右孩子结点的值。

如果满足每个结点的值都大于其左孩子和右孩子结点的值，则是大根堆（大顶堆）；

如果满足每个结点的值都小于其左孩子和右孩子结点的值，则是小根堆（小顶堆）。

总结就是：

堆是一种特殊的树，只要满足下面两个条件，它就是一个堆：

（1）堆是一颗完全二叉树；

（2）堆中某个节点的值总是不大于（或不小于）其父节点的值。

算法思想

通过将无序表转化为堆，可以直接找到表中最大值或者最小值，然后将其提取出来，令剩余的记录再重建一个堆，取出次大值或者次小值，如此反复执行就可以得到一个有序序列，此过程为堆排序。

以利用大根堆排序为例：

（1）首先将待排序列\(a[1…n]\)调整为大根堆（此过程为建初堆），交换\(a[1]\)和\(a[n]\)，则\(a[n]\)为关键字最大的记录

（2）将\(a[1…n-1]\)重新调整为大根堆，交换\(a[1]\)和\(a[n-1]\)，则\(a[n-1]\)为关键字次大的记录

（3）循环\(n-1\)次，直到交换了\(a[1]\)和\(a[2]\)，得到一个非递减的有序序列\(a[1…n]\)

堆排序过程的代码实现需要解决两个问题：

1. 如何将得到的无序序列转化为一个堆？
2. 在输出堆顶元素之后（完全二叉树的树根结点），如何调整剩余元素构建一个新的堆？

大根堆建堆

① 从最后一个分支结点开始，与其孩子结点的值比较。如果不符合特性，则交换；如果是大根堆，选择孩子结点中的较大值

② 交换之后如果孩子结点也是分支结点，继续向下比较；

③ 反复利用上述过程构造下一级的堆，直至根结点。

大根堆建堆过程演示

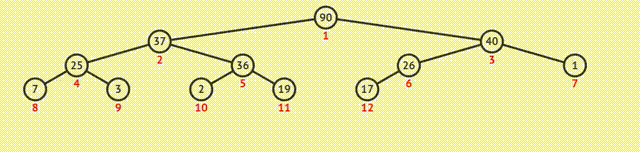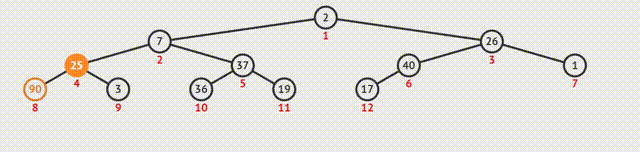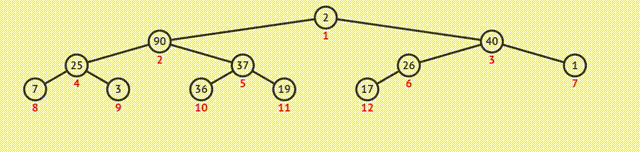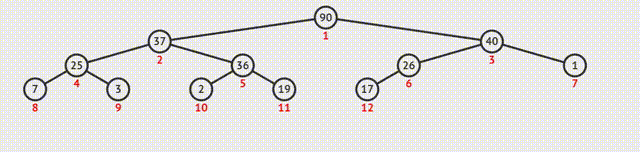
如何调整剩余元素构建一个新的堆

① 输出堆顶元素后，将最后一个元素与之交换，此时堆的结构特性被破坏，需要向下筛选；

② 从上向下逐级比较，使每一级都符合特性。

堆排序过程演示

算法分析

空间负责度：使用常数个辅助单元，空间复杂度为\(O(1)\)

时间复杂度：建堆时间为\(O(n)\)，之后有n-1次向下调整，调整操作的时间复杂度为\(O(h)\)也就是\(O(log_2n)\)，所以堆排序的时间复杂度为\(O(n*log_2n)\)。

稳定性：不稳定

适用性：适用于线性表为顺序存储的情况，不能用于链式结构

优点：初始建堆所需比较次数较多，因此对小文件效果不明显，但对大文件有效

堆排序在最坏情况下时间复杂度为\(O(n*log_2n)\)，对于快速排序最坏情况下的\(O(n^2)\)言是一个优点，当记录较多时较为高效

算法代码

#include <stdio.h>

#define MAXSIZE 100 // 定义堆的最大长度

typedef struct {
    int key; // 关键字
} ElemType;

typedef struct {
    ElemType r[MAXSIZE]; // 用于存储堆元素的数组
    int length; // 当前堆的长度
} SqList;

// 函数声明
void HeapAdjust(SqList &H, int s, int m);
void HeapSort(SqList &H);
void printArray(SqList &H);

int main() {
    SqList H;
    H.length = 0;

    // 初始化堆元素
    printf("请输入堆的长度：");
    scanf("%d", &H.length);
    printf("请输入堆元素的关键字：");
    for (int i = 1; i <= H.length; ++i) {
        scanf("%d", &H.r[i].key);
    }

    // 执行堆排序
    HeapSort(H);

    // 打印排序后的堆元素
    printf("堆排序后的结果：\n");
    printArray(H);

    return 0;
}

// 函数：对以s为根的子树进行堆调整，m为子树的长度
void HeapAdjust(SqList &H, int s, int m) {
    ElemType rc = H.r[s]; // 当前堆顶记录
    int j;

    for (j = 2 * s; j <= m; j *= 2) {
        if (j < m && H.r[j].key < H.r[j + 1].key) {
            ++j; // j为key较大的儿子记录下标
        }
        if (!(rc.key < H.r[j].key)) {
            break;
        }
        H.r[s] = H.r[j];
        s = j;
    }
    H.r[s] = rc; // 原堆顶记录交换到s位置
}

// 函数：堆排序
void HeapSort(SqList &H) {
    int i;
    ElemType temp;

    // 将H.r[1..H.length]建成大顶堆
    for (i = H.length / 2; i > 0; --i) {
        HeapAdjust(H, i, H.length);
    }

    // 将堆顶记录和当前子序列最后一个记录交换，然后重新调整为大顶堆
    for (i = H.length; i > 1; --i) {
        temp = H.r[1];
        H.r[1] = H.r[i];
        H.r[i] = temp;
        HeapAdjust(H, 1, i - 1);
    }
}

// 函数：打印数组
void printArray(SqList &H) {
    for (int i = 1; i <= H.length; i++) {
        printf("%d ", H.r[i].key);
    }
    printf("\n");
}

基数排序

算法思想

基数排序是一种很特别的排序，它不基于比较和移动，而是基于各个位上关键字的大小进行排序。

假设长度为n的线性表由d元组\((k_{d-1}, k_{d-2}, …, k_1, k_0)\)组成，其中\(k_{d-1}\)为最主位关键字，\(k_0\)为最次位关键字。

关键字排序有两种方法：

①最高位优先法(MSD)：按关键字权重递减依次逐层划分成子序列，然后依次连接成有序序列。

②最低位优先法(LSD)：按关键字权重递增依次逐层划分成子序列，然后依次连接成有序序列。

MSD( Most Significant Digit ) LSD ( Least Significant Digit )

由于整数也可以表达字符串（比如名字或日期）和特定格式的浮点数，所以基数排序也不是只能使用于整数。

LSD 基数排序动图演示

LSD 基数排序动图演示

算法分析

代码实现

参考：

1.0 十大经典排序算法 | 菜鸟教程 (runoob.com)

hustcc/JS-Sorting-Algorithm: 一本关于排序算法的 GitBook 在线书籍 《十大经典排序算法》，多语言实现。 (github.com)

数据结构各内部排序算法总结对比及动图演示（插入排序、冒泡和快速排序、选择排序、堆排序、归并排序和基数排序等）2-阿里云开发者社区 (aliyun.com)

【数据结构】内部排序-CSDN博客