算法-5-贪心算法

最优化问题

一般特征：问题有n个输入，问题的解是由这n个输入的某个子集组成，这个子集必须满足某些事先给定的条件。

• 约束条件：子集必须满足的条件

• 可行解：满足约束条件的子集；可行解可能不唯一

• 目标函数：用来衡量可行解优劣的标准，一般以函数形式给出

• 最优解：能够使目标函数取极值 (极大或极小)的可行解、

最优化问题求解分类：根据描述问题约束条件和目标函数的数学模型的特性和问题的求解方法的不同，可分为：线性规划、整数规划、非线性规划、动态规划、分支限界法等精确算法

贪心方法：一种改进的分级的处理方法，可对满足上述特征的某些问题方便地求解，属于近似算法。即每次在做选择时，总是先选择具有相同特征的那个解，即“贪心解”

贪心算法

概述

当某问题具有最优子结构性质时，可用动态规划法求解(精解确、大规模等问题效率低)，但有时用贪心算法求解会更简单、更有效。

顾名思义，贪心算法总是作出在当前看来最好的选择，并不从整体最优考虑，它所作出的选择只是在某种意义上的局部最优选择。当然，其希望得到的最终结果是整体最优的。

虽然不能对所有问题都得到整体最优解，但对许多问题它能产生整体最优解。如单源最短路经问题，最小生成树问题等。在一些情况下，贪心算法不能得到整体最优解，但其最终结果是最优解的近似。

基本思想

• 从问题的某一个初始解出发，通过一系列的贪心选择，即当前状态下的局部最优选择，逐步逼近给定的目标，尽可能快地求得更好的解。
• 在贪心算法(Greedy Method)中采用逐步构造/分级最优解的方法。在每个阶段，都作出一个按某个评价函数最优的决策，该最优评价函数称为贪心准则(Greedy Criterion)
• 贪心算法的正确性，要证明按贪心准则求得的解是全局最优解

基本步骤

1. 决定问题的最优子结构
2. 设计出一个递归解
3. 证明在递归的任一阶段，最优选择之一总是贪心选择，那么做贪心选择总是安全的。
4. 证明通过做贪心选择，所有子问题(除一个以外)都为空，即只产生一个子问题
5. 设计出一个实现贪心策略的递归算法。
6. (性能角度) 将递归算法转换成迭代算法。

贪心算法的基本要素

对于一个具体的问题，怎么知道是否可用贪心算法解此问题，以及能否得到问题的最优解呢？这个问题很难给予肯定的回答。但是，从许多可以用贪心算法求解的问题中看到这类问题一般具有2个重要的性质：贪心选择性质和最优子结构性质

贪心选择性质

所谓贪心选择性质是指所求问题的整体最优解可以通过一系列局部最优的选择，即贪心选择来达到。这是贪心算法可行的第一个基本要素，也是贪心算法与动态规划算法的主要区别。

动态规划算法通常以自底向上的方式解各子问题，而贪心算法则通常以自顶向下的方式进行，以迭代的方式作出相继的贪心选择，每作一次贪心选择就将所求问题简化为规模更小的子问题。

对于一个具体问题，要确定它是否具有贪心选择性质，必须证明每一步所作的贪心选择最终导致问题的整体最优解，否则得到的是近优解。

最优子结构性质

当一个问题的最优解包含其子问题的最优解时，称此问题具有最优子结构性质。

问题的最优子结构性质是该问题可用动态规划算法或贪心算法求解的关键特征。但是，需要注意的是，并非所有具有最优子结构性质的问题都可以采用贪心策略来得到最优解

贪心算法只需考虑一个选择(即贪心的选择)；在做贪心选择时，子问题之一必须是空的，因此只留下一个非空子问题。（是什么意思🙄

贪心算法 vs 动态规划

贪心算法和动态规划算法都要求问题具有最优子结构性质，但是两者存在着巨大的差别

(1)动态规划是先分析子问题，再做选择。而贪心算法是先做贪心选择，做完选择后，生成子问题，然后再去求解子问题

2. 动态规划每一步可能会产生多个子问题，而贪心算法每一步只会产生一个子问题(为非空)

(3)从特点上看，动态规划是自底向上解决问题，而贪心算法是自顶向下解决问题

与递归、分治的联系

分治策略用于解决原问题与子问题结构相似的问题，对于各子问题相互独立的情况，一般用递归实现

动态规划用于解决子问题有重复求解的情况，既可以用递归实现，也可以用迭代实现

贪心算法用于解决具有贪心选择性质的问题，既可以用递归实现，也可以用迭代实现，因为很多递归贪心算法都是尾递归，很容易改成迭代贪心算法

递归是实现手段，分治策略是解决问题的思想，动态规划和贪心算法很多时候会使用记录子问题运算结果的递归实现

最小生成树—Prim算法

最小生成树问题

问题描述

• 设\(G=(V,E)\)是无向连通带权图，即一个网络。（V是顶点集合，E是边集合，E中每条边(v,w)的权为\(c[v][w]\)）。
• 如果G的子图G’是一棵包含G的所有顶点的树，则称G’为G的生成树。生成树上各边权的总和称为该生成树的耗费。
• 在G的所有生成树中，耗费最小的生成树称为G的最小生成树(MST: minimumcost spanning tree)

Prim算法和Kruskal算法：都是解最小生成树问题的贪心算法；它们做贪心选择的方式不同，但都利用了下面的最小生成树性质。

最小生成树性质

• 设\(G=(V,E)\)是连通带权图，U是V的真子集。
• 如果\((i,j)∈E\)，且\(i∈U，j∈V-U\)，且在所有这样的边中，\((i,j)\)的权\(c[i][j]\)最小，那么必存在一棵包含边\((i,j)\)的最小生成树。
• 这个性质也称为MST（Minimum Spanning Tree）性质。

Prim算法

贪心选择策略： 每次都选择到下一顶点权最小的边。

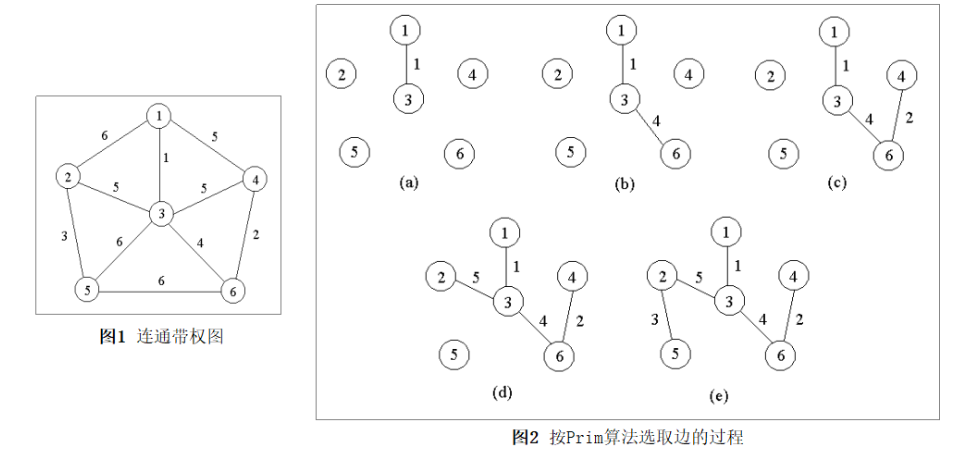
普里姆算法的实现思路是：

1. 将连通网中的所有顶点分为两类（假设为 A 类和 B 类）。初始状态下，所有顶点位于 B 类；
2. 选择任意一个顶点，将其从 B 类移动到 A 类；
3. 从 B 类的所有顶点出发，找出一条连接着 A 类中的某个顶点且权值最小的边，将此边连接着的 A 类中的顶点移动到 B 类；
4. 重复执行第 3 步，直至 B 类中的所有顶点全部移动到 A 类，恰好可以找到 N-1 条边。

Prim算法例子

代码实现

真的有点难度吧哥

普里姆算法(Prim算法)求最小生成树 (biancheng.net)

克鲁斯卡尔算法(Kruskal算法)求最小生成树 (biancheng.net)

flags轲限梭畴坫他浛
0264D9A0                                                                                                   66                                  f
0264D9C0   6C 61 67 73 E9 F0 CF DE  FE 8F FD F3 CB F3 AB FB  B3 EB DB E3 CB FB 9B BF                            lags轲限?梭畴坫他浛