算法 6 回溯法

1

方法概述

搜索算法介绍

1. 穷举搜索

2. 盲目搜索

• 深度优先( DFS ) 或 回溯搜索 (Backtracking)；
• 广度优先搜索(BFS)；
• 分支限界法(Branch & Bound)
• 博奔树搜索 (α-β Search)

3. 启发式搜索

• A* 算法和最佳优先(Best-First Search)

• 迭代加深的A* 算法

• B* ，AO* ，SSS*等算法

• Local Search，GA等算法

搜索空间的三种表示

表序表示：搜索对象用线性表数据结构表示

显示图表示：搜索对象在搜索前就用图(树)的数据结构表示

隐式图表示：除了初始结点，其他结点在搜索过程中动态生成。缘于搜索空间大，难以全部存储。

回溯法(Backtracking)

回溯法(Backtracking)又称为试探法：

• 回溯法是一个既带有系统性又带有跳跃性的搜索算法；
• 它在包含问题的所有解的解空间树中，按照深度优先的策略，从根结点出发搜索解空间树。—— 系统性
• 算法搜索至解空间树的任一结点时，判断该结点为根的子树是否包含问题的解，如果肯定不包含，则跳过以该结点为根的子树的搜索逐层向其祖先结点回溯。否则，进入该子树，继续深度优先的策略进行搜索。——跳跃性
• 这种以深度优先的方式系统地搜索问题的解的算法称为回溯法。它适用于解一些组合数较大的问题。许多复杂的、规模较大的问题都可以使用回溯法，有“通用解题方法”的美称。
• 递归(Recursion)、迭代(lteration)、回溯??区别与联系

基本思想

（上面的概念也是属于基本思想的）

• 搜索从开始结点(根结点) 出发，以深度优先搜索整个解空间。
• 这个开始结点成为活结点，同时也成为当前的扩展结点。在当前的扩展结点处，搜索向纵深方向移至一个新结点。这个新结点就成为新的活结点，并成为当前扩展结点。
• 如果在当前的扩展结点处不能再向纵深方向扩展，则当前扩展结点就成为死结点。
• 此时，应往回移动(回溯)至最近的一个活结点处(回溯点)，并使这个活结点成为当前的扩展结点;直到找到一个解或全部解。

基本步骤：

1. 针对所给问题，定义问题的解空间；
2. 确定易于搜索的解空间结构；
3. 以深度优先方式搜索解空间，并在搜索过程中用前枝函数避免无效搜索。

常用剪枝函数：

① 用约束函数在扩展结点处剪去不满足约束的子树；

② 用限界函数剪去得不到最优解的子树。

二类常见的解空间树：

子集树

当所给的问题是从n个元素的集合S中找出满足某种性质的子集时，相应的解空间树称为子集树。子集树通常有\(2^n\)个叶子结点，其总结点个数为\(2^{n+1}-1\)，遍历子集树时间为\(Ω(2^n)\)。如0-1背包问题，叶结点数为\(2^n\)，总结点数\(2^{n+1}\)。

假设现在有一列数 \(a[0],a[1], ...a[n-1]\)，如果一个问题的解的长度不是固定的，并且解和元素顺序无关，即可以从中选择0个或多个，那么解空间的个数将是指数级别的，为\(2^n\),可以用下面的子集树来表示所有的解(假设这里n=4)

子集树

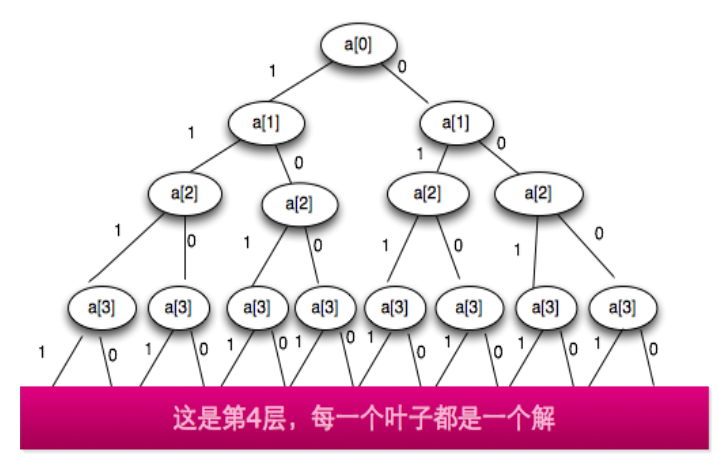
这里一共有\(2^4=16\)种情况

0-1背包问题（1）

0-1背包问题（2）

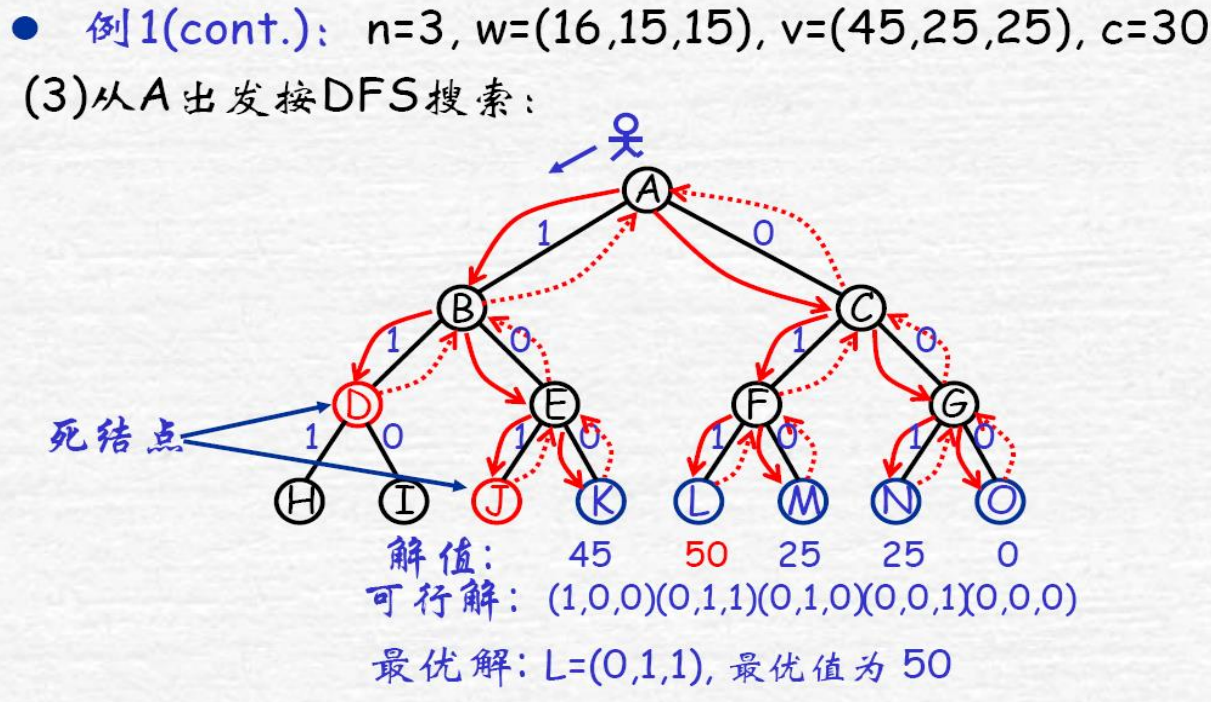
排列树

当所给问题是确定n个元素满足某种性质的排列时，相应的解空间树称为排列树。排列树通常有\(n!\)个叶子结点，因此，遍历排列树需要\(Ω(n!)\)的计算时间。如TSP问题(Traveling Salesman Problem，推销员问题)，叶结点数为\(n!\)，遍历时间为\(Ω(n!)\)。

如果解空间是由n个元素的排列形成，即n个元素的每一个排列都是解空间中的一个元素，那么，最后解空间的组织形式是排列树。

排列树

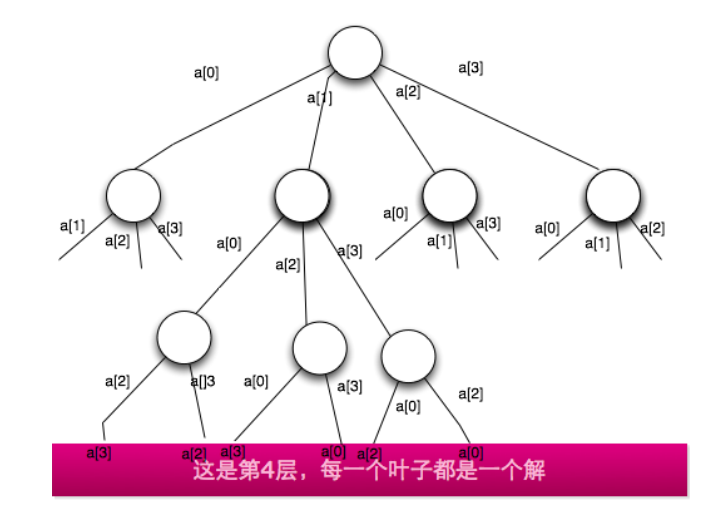
这里每一个元素有\(3*2*1=6\)种情况，一共就有\(4*6=24\)种情况，也就是\(4*3*2*1=24\)

TSP问题

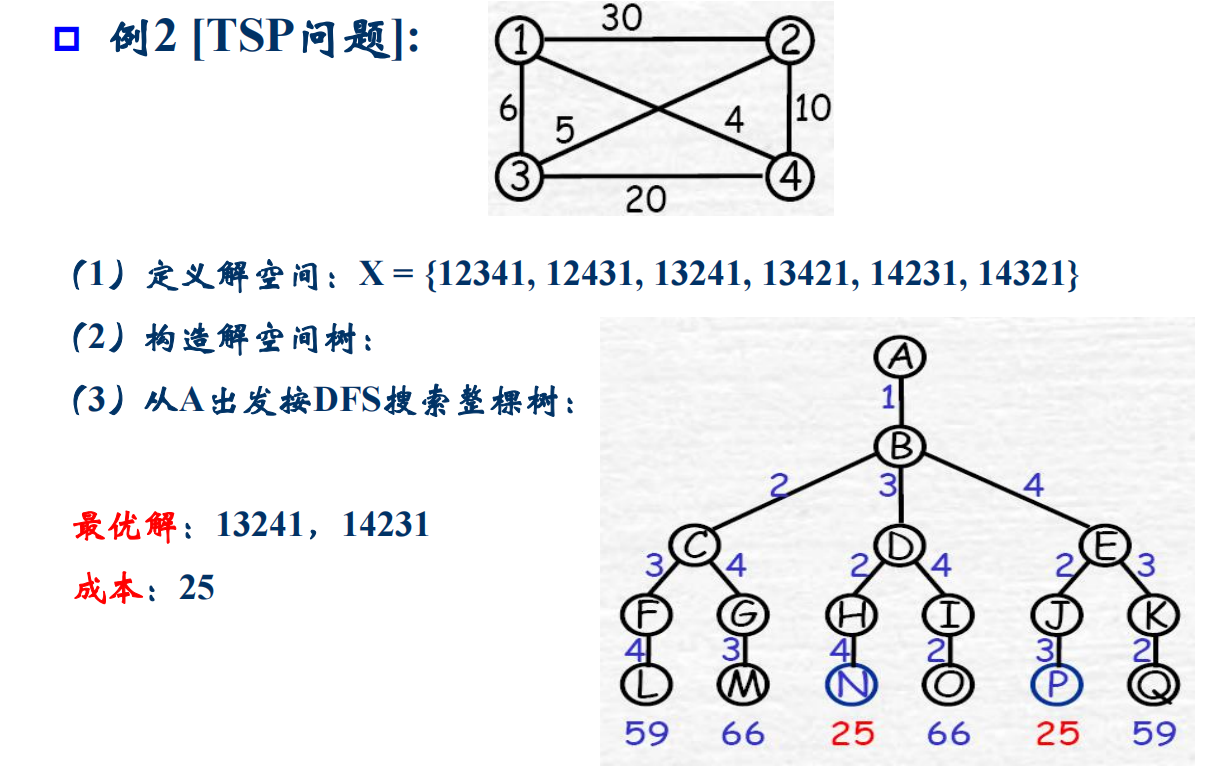
因为这里规定了从A出发，所以一共就有\(3*2*1=6\)种情况

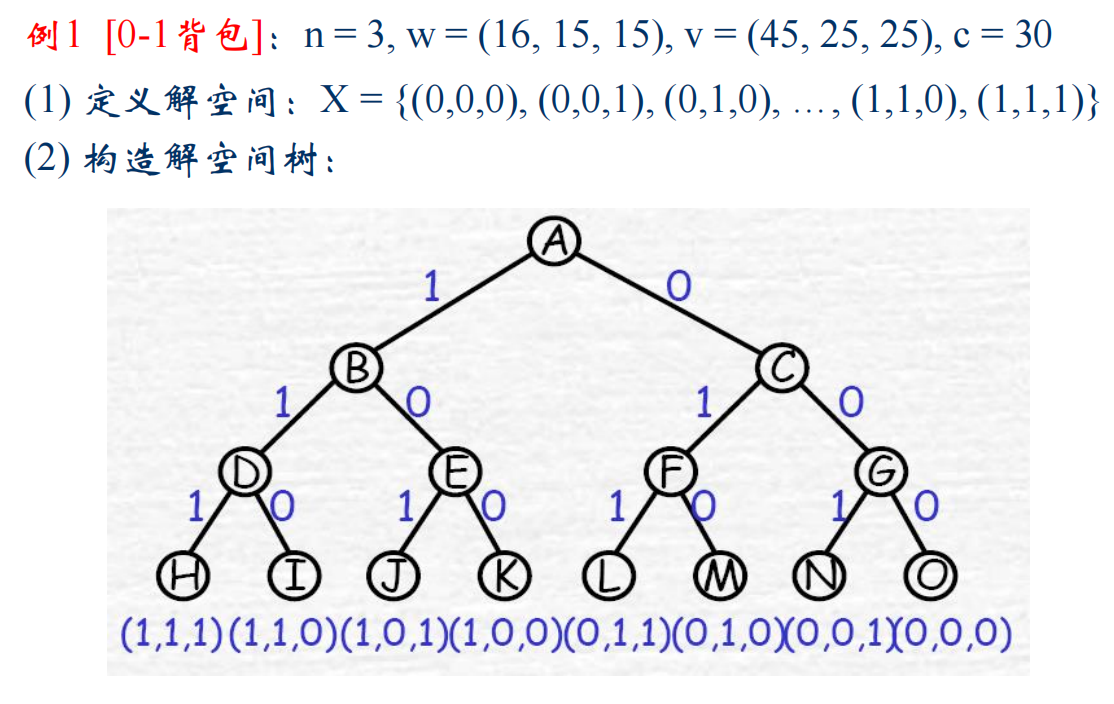
0-1背包问题

问题描述

给定n种物品和一背包。物品i的重量是\(w_i>0\)，其价值为\(v_i>0\)，背包的容量为c。问应如何选择装入背包中的物品，使得装入背包中物品的总价值最大？

如：

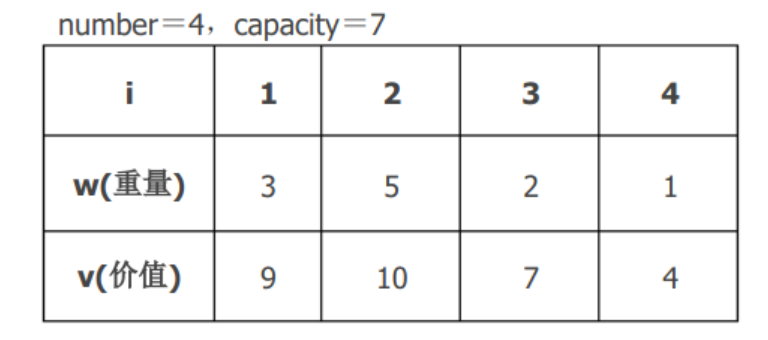
肉眼可算出答案是[1,3,4]，结果是20

复杂度分析

时间复杂度分析：

回溯法的时间复杂度通常随着问题规模的增加而指数级增长。在每一步，算法需要考虑选择或不选择当前物品，因此复杂度为 \(O(2^n)\)，其中 n 是物品的数量。这是因为对于每个物品，都有两种选择：选择或不选择。因此，总共有 \(2^n\) 种组合需要考虑。

空间复杂度分析：

空间复杂度主要取决于递归调用的深度。在回溯法中，递归调用堆栈的深度是问题的规模。因为在每一步中都有两个分支（选择或不选择），递归树的深度是 n，其中 n 是物品的数量。因此，空间复杂度为 \(O(n)\)。

需要注意的是，这里的空间复杂度并不考虑输入数据的空间占用，仅仅是算法本身的空间占用。

需要注意的是，虽然回溯法的时间复杂度很高，但在实际应用中，可以通过一些优化策略（例如剪枝）来减少搜索空间，提高算法效率。对于0-1背包问题，通常更推荐使用动态规划来获得更高效的解决方案。

代码

python：

要我说，这玩意真要好好调试一下吧，不然🐭🐭是真理解不了啊

这真有人第一次能自己写出来吗，我怎么不信呢😭😭😭

# python
max_V, now_W, now_V, best_X, goods = 0, 0, 0, [], []  # 最大价值、当前重量、当前价值、最优解、商品列表
print('请输入物品数量、背包容量，空格隔开：')
n, c = map(int, input().split())
for i in range(n):
    print(f'请输入第{i + 1}个物品的重量和价值，空格隔开：')
    goods.append(list(map(int, input().split())))
x = [0 for i in range(n)]  # 初始化当前解


def backtrack(i):  # i是层数，n个物品，共有n+1层
    global max_V, now_V, now_W, best_X, x  # 引入全局变量
    if i >= n:  # 当层数超过物品总数量的时候
        if max_V < now_V:  # 当最大值小于当前价值时，更新最大值
            max_V = now_V
            best_X = x[:]  # 同步更新最优解
    else:
        if now_W + goods[i][0] <= c:  # 如果当前重量加上该层对应物品的重量，可以装在背包里
            x[i] = 1  # 那么就装入这个物品（当前物品的状态为1）
            now_W += goods[i][0]  # 更新当前重量和价值
            now_V += goods[i][1]
            backtrack(i + 1)  # 进入下一个节点（如果符合条件就到底了）
            now_W -= goods[i][0]  # 另一侧节点
            now_V -= goods[i][1]
        x[i] = 0  # 初始化物品状态
        backtrack(i + 1)  # 进入下一层


backtrack(0)  # 从第0层开始搜索
print(f'最大价值为：{max_V}')
print(f'应装物品编号为：{[i + 1 for i in range(n) if best_X[i]]}')

0-1背包问题 —— 四种解法解题 - Shaw_喆宇 - 博客园 (cnblogs.com)