算法 7 分支界限法

方法概述部分基本为老师PPT的内容，我™也有点看不懂，不知道是我太菜了，还是PPT不清楚🤧🤧🤧

方法概述

与回溯法区别

• 求解目标不同

  一般而言，回溯法的求解目标是找出解空间树中满足约束条件的所有解，而分支限界法的求解目标则是尽快地找出满足约束条件的一个解

• 搜索方法不同

  回溯法使用深度优先方法搜索，而分支限界一般用宽度优先或最佳优先方法来搜索

• 对扩展结点的扩展方式不同

  分支限界法中，每一个活结点只有一次机会成为扩展结点。活结点一旦成为扩展结点，就一次性产生其所有儿子结点;

• 存储空间的要求不同

  分支限界法的存储空间比回溯法大得多，因此当内存容量有限时，回溯法解决问题成功的可能性更大。

分支界限法基本思想

以广度优先或最小耗费（最大效益）优先的方式搜索问题的解空间树

• 每个活结点只有一次机会成为扩展结点并一次性产生其所有儿子结点
• 儿子结点中导致不可行解或非最优解的儿子结点被舍弃，其余儿子结点被加入活结点表中。如是最小耗费优先，活结点表需要重新排序
• 此后从活结点表中取下一结点成为当前扩展结点，并重复上述结点扩展过程。这个过程一直持续到找到所需的解或活结点表为空时为止

分支限界法常以广度优先或以最小耗费（最大效益）优先的方式搜索问题的解空间树。 1. 对已处理的各结点根据限界函数估算目标函数的可能取值 2. 从中选出目标函数取得极大(极小) 值的结点优先进行广度优先搜索 3. 不断地调整搜索方向，尽快找到解，裁剪那些不能得到最优解的子树以提高搜索效率

搜索策略：

在扩展结点处，首先生成其所有的儿子结点（分支），然后从当前的活结点表中选择下一个扩展结点。 思考：如何代码实现？

为了有效地选择下一个扩展结点，以加速搜索的进程，在每一个活结点处，计算一个函数值(优先值)，并根据这些已计算出的函数值，从当前活结点表中选择一个最有利的结点作为扩展结点，使搜索朝着解空间树上有最优解的分支推进，以便尽快地找出一个最优解。

Branch and Bound求解步骤：

1. 定义解空间（对解编码）
2. 确定解空间的树结构
3. 按BFS等方式搜索
   1. 每个活结点仅有一次机会变成扩展结点
   2. 由扩展结点生成一步可达（即宽度搜索）的新结点C
   3. 在新结点中，删除不可能导出最优解的结点； // 限界策略
   4. 将剩余的新结点加入活动表（队列）中
   5. 从活动表中选择结点再扩展； //分支策略
   6. 直至活动表为空

常见的两种分支限界法

image-20231206172054010

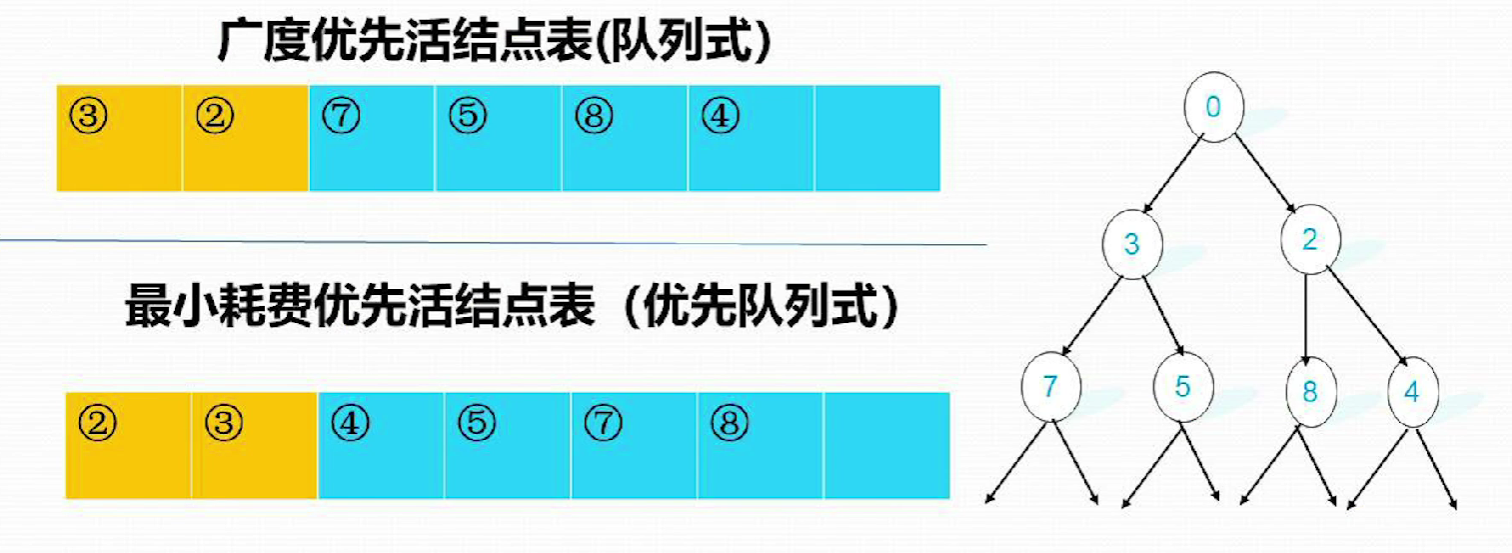
队列式（FIFO）分支限界法

• 按照队列先进先出（FIFO）原则选取下一个结点为扩展结点
• 从活结点表中取出结点的顺序与加入结点的顺序相同，因此活结点表的性质与队列相同

优先队列分支限界法（代价最小或效益最大）

• 每个结点都有一个对应的耗费或收益，以此决定结点的优先级
• 从优先队列中选取优先级最高的结点成为当前扩展结点
• 如果查找一个具有最小耗费的解：则活结点表可用小顶堆来建立，下一个扩展结点就是具有最小耗费的活结点
• 如果希望搜索一个具有最大收益的解：则可用大顶堆来构造活结点表，下一个扩展结点是具有最大收益的活结点

0-1背包问题

队列式（FIFO）分支限界法

队列式（FIFO）分支限界法解决0-1背包问题

image-20231206153332482

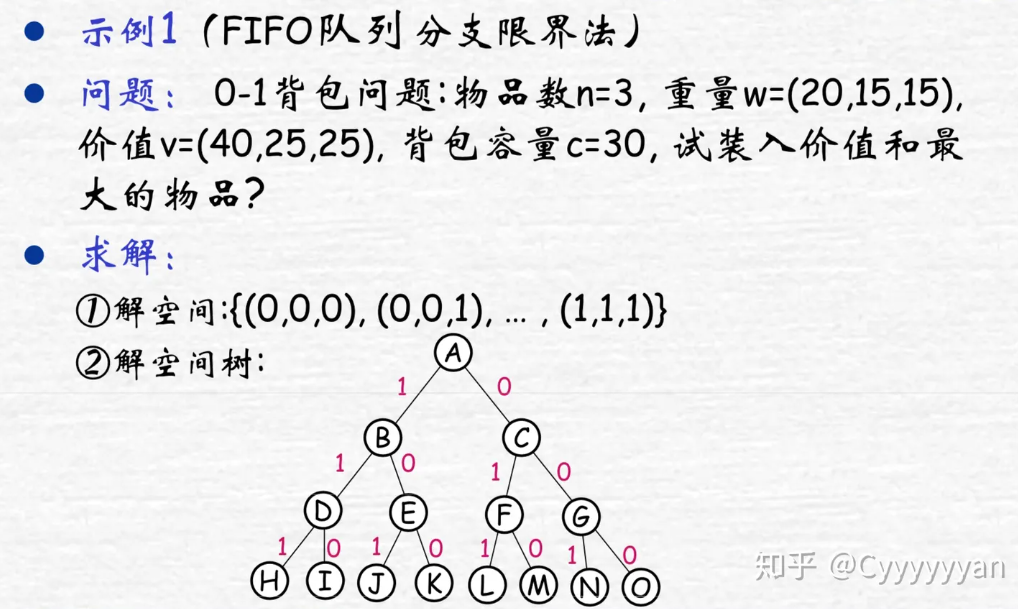
通过判断重量加起来是否超过背包容量来判断是不是死节点

步骤：

① 用一个队列存储活结点表，初始为空

② A为当前扩展结点，其儿子结点B和C均为可行结点，将其按从左到右顺序加入活结点队列，并舍弃A。

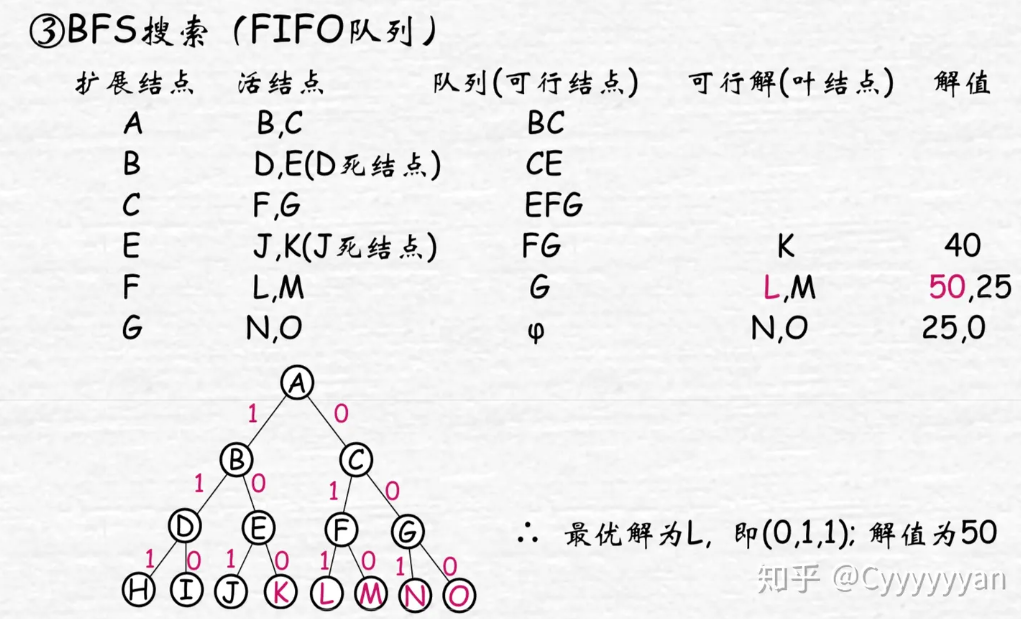
③ 按FIFO原则，下一扩展结点为B，其儿子结点D不可行，舍弃；E可行，加入。舍弃B

④ C为当前扩展结点，儿子结点F、G均为可行结点，加入活结点表，舍弃C

⑤ 扩展结点E的儿子结点J不可行而舍弃；K为可行的叶结点，是问题的一个可行解，价值为45

⑥ 当前活结点队列的队首为F, 儿子结点L、M为可行叶结点，价值为50、25

⑦ G为最后一个扩展结点，儿子结点N、O均为可行叶结点，其价值为25和0

⑧ 活结点队列为空，算法结束，其最优值为50

注：活结点就是不可再进行扩展的节点，也就是两个儿子还没有全部生成的节点

优先队列分支限界法

优先队列分支限界法求解0-1背包问题

image-20231206155119099

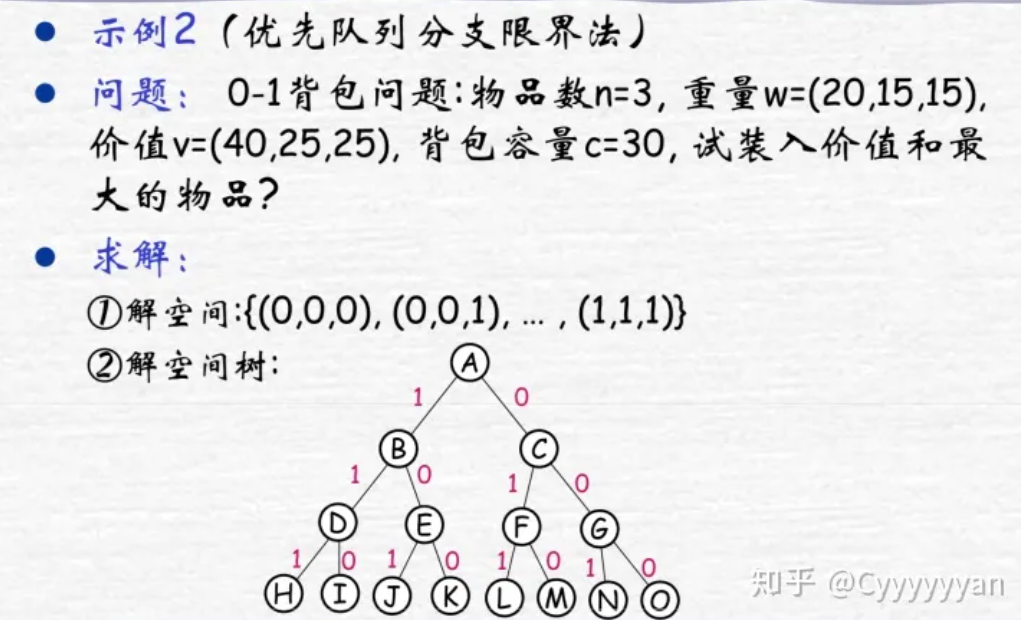
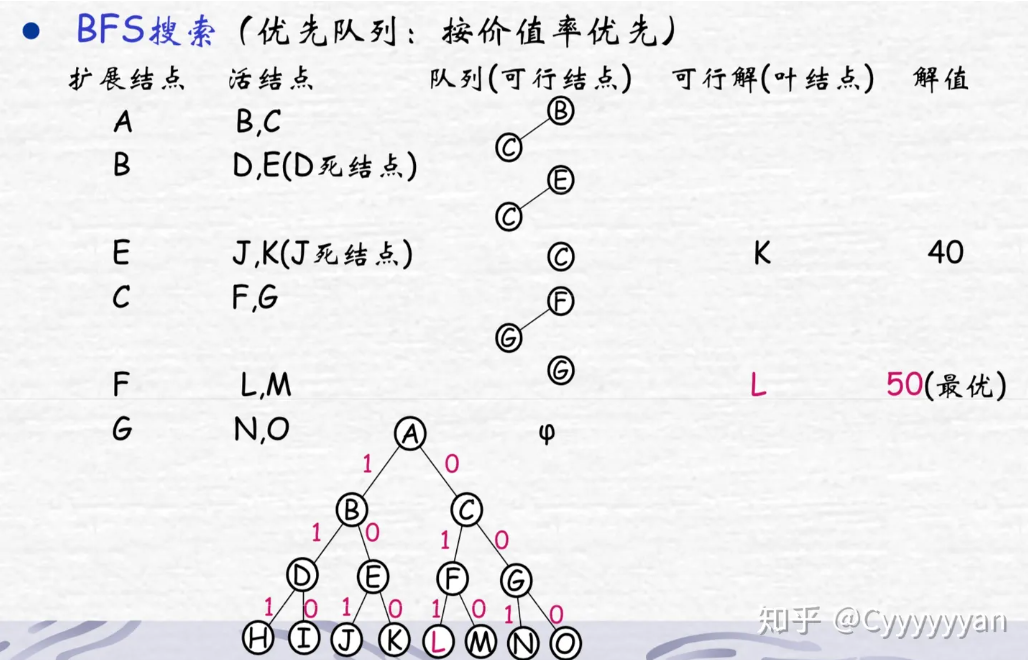
步骤：

① 用一个极大堆表示活结点表的优先队列，其优先级定义为活结点所获得的价值。初始为空。

② 由A开始搜索解空间树，其儿子结点B、C为可行结点，加入堆中，舍弃A。

③ B获得价值40，C为0。B为堆中价值最大元素，并成为下一扩展结点。

④ B的儿子结点D是不可行结点，舍弃。E是可行结点，加入到堆中。舍弃B。

⑤ E的价值为40，是堆中最大元素，为当前扩展结点。

⑥ E的儿子J是不可行叶结点，舍弃。K是可行叶结点，为问题的一个可行解价值为40。

⑦ 继续扩展堆中唯一活结点C，直至存储活结点的堆为空，算法结束。

⑧ 算法搜索得到最优值为50，最优解为从根结点A到叶结点L的路径（0，1，1）。

//优先队列分支限界法解决0-1背包问题
branchknap(float w[],float v[]){
    根结点入队
    while(队列不为空){
        Node *current = 单位重量价值最大元素出队//扩展结点
 
        if(current为叶子结点){
            if(current路径能得到最优值)
                更新bestv和bestx;
        }
        else{
            if(current的左孩子可行并有可能产生最优解)
                左孩子入队
            if(current的右孩子有可能产生最优解)
                右孩子入队
        }
	}
}

分支限界法 0-1背包问题-队列式 - 沅清的小窝 - 博客园 (cnblogs.com)

参考：

分支限界法解决01背包问题 - boobo - 博客园 (cnblogs.com)