本文最后更新于:2023年12月23日 晚上
根据b站王卓老师的课程记录的学习笔记📕
现在已经实现顺序栈的各种操作,
还有链栈、队列
3.1 栈和队列的定义和特点
栈和队列是两种重要的线性结构。栈和队列是限定插入和删除只能在表的“端点”进行的线性表。
由于栈的操作具有后进先出 的固有特性,使栈成为程序设计中有用的工具。另外,如果问题求解过程中具有“后进先出”的天然特性,则求解的算法中必须利用栈
数制转换 表达式求值 括号匹配的检验 八皇后问题 行编辑程序 函数调用
迷宫求解 递归调用的实现
由于队列的操作具有先进先出 的特性,使得队列成为程序设计中解决类似排队问题的有用工具。
脱机打印输出按申请的先后顺序依次输出
多用户系统中多个用户排成队,分时地循环使用CPU和主存
按用户的优先级排成多个队,每个优先级一个队列
实时控制系统中信号按接收的先后顺序依次处理
网络电文传输按照到达时间的先后顺序依次进行
栈和队列的基本操作是线性表操作的子集,它们是操作受限的线性表,因此,可称为限定性的数据结构。
3.1.1 栈的定义和特点
1. 栈的定义
栈(stack):是一个特殊的线性表,是限定仅在一端(通常是表尾)进行插入或删除操作的线性表。
又称后进先出(Last In First Out)的线性表,简称LIFO结构
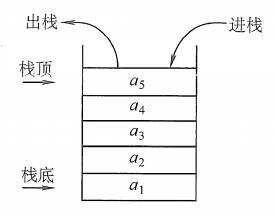
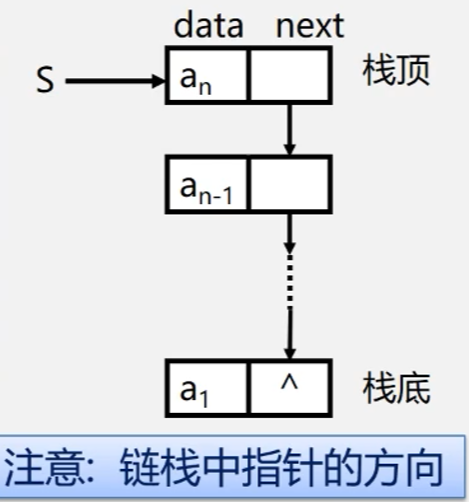
栈
2. 栈的相关概念
栈 是仅在表尾进行插入、删除操作的线性表
表尾 (即\(a_n\) 端) 称为栈顶
Top;表头 (即\(a_1\) 端)
称为栈底Base
例如:栈
s = (a, a2, a3,....., an-1, an),a1称为栈底元素,an称为栈顶元素
插入元素到栈顶 (即表尾) 的操作,称为入栈或进栈或压栈
从栈顶 (即表尾) 删除最后一个元素的操作,称为出栈或弹栈
入 = 压入 = PUSH (x),出 = 弹出 = POP (y)
栈的小结:
定义:限定只能在表的一端进行插入和删除操作运算的线性表(只能在栈顶操作)
逻辑结构:同线性表一样栈元素具有线性关系即前驱后继关系(一对一)
存储结构:顺序栈和链栈均可,顺序栈更常见
运算规则:只能在栈顶运算,且访问结点时依照后进先出的原则(LIFO)
实现方式:关键是编写入栈和出栈函数,具体实现依顺序栈和链栈的不同而不同
栈和线性表唯一的区别在于运算规则。线性表插入删除位置任意而栈只能对表尾(栈顶)的元素进行插入和删除操作。
3.1.2 队列的基本概念
1. 队列的定义
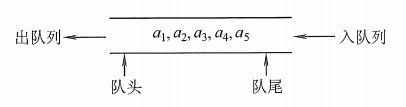
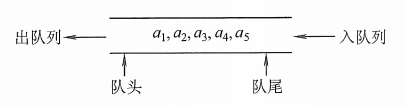
队列(queue)是只允许在一端进行插入操作,而在另一端进行删除操作的线性表。
队列是一种先进先出(First In First
Out)的线性表,简称FIFO。允许插入的一端称为队尾,允许删除的一端称为队头。
队头(Front):允许删除的一端,又称队首。
队尾(Rear):允许插入的一端。
队列
2. 队列的相关概念
队列的总结:
定义:只能在表的一端进行插入运算在表的另一端进行删除操作运算的线性表
(头删尾插)
逻辑结构:同线性表一样,仍为一对一关系
存储结构:顺序队和链队均可,以循环顺序队列更常见
运算规则:只能在队首和队尾运算,且访问结点时依照先进先出的原则(FIFO)
实现方式:关键是掌握入队和出队操作,具体实现依顺序队和链队的不同而不同
3.2 案例引入
进制转换
括号匹配的检验
表达式求值
舞伴问题
3.3 栈的表示和操作的实现
3.3.1 栈的抽象数据类型的定义
1 2 3 4 5 6 ADT Stack{1 ,2 ,…n;n≥0 }-1 ,ai>|ai-1 ,ai∈D,i=2 ,…n},约定an端为栈顶,a1端为栈底
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 InitStack (&S) DestroyStack (&S) StackEmpty (S) StackLength (S) GetTop (S, &e) ClearStack (&S) Push (&S, e) Pop (&S, &e)
由于栈本身就是线性表,于是栈也有顺序栈和链栈两种实现方式
栈的顺序存储——顺序栈
栈的链式存储——链栈
3.3.2 顺序栈的表示和实现
1. 顺序栈的概述
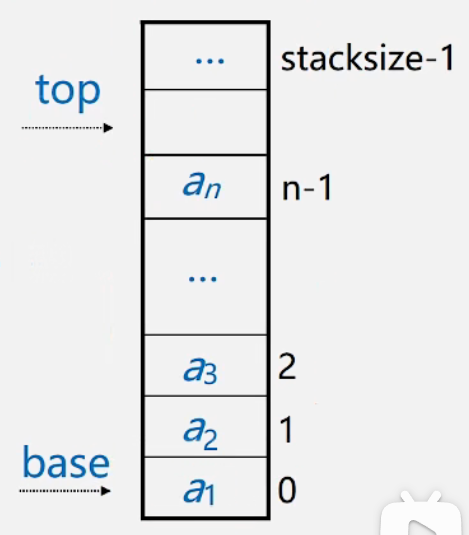
存储方式:同一般的线性表的顺序存储结构完全相同,
利用一组地址连续的存储单元(数组)依次存放自栈底到栈顶的数据元素,栈底一般在低地址端
栈的结构
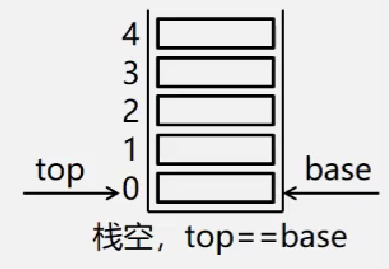
空栈:base == top 是栈空标志
栈满:top-base==stacksize
栈满时的处理方法:
报错,返回操作系统
分配更大的空间,作为栈的存储空间,将原栈的内容移入新栈
使用数组作为顺序栈存储方式的特点:简单、方便、但易产生溢出(数组大小固定)
上溢(overflow):栈已经满,又要压入元素
下溢(underflow):栈已经空,还要弹出元素
注:上溢是一种错误,使问题的处理无法进行;而下溢一般认为是一种结束条件,即问题处理结束。
2. 顺序栈的实现
1 2 3 4 5 6 #define MAXSIZE 100 typedef struct {int stacksize;
top和base可以定义为整型存储数组的下标或者定义为指针 (指针相减的前提是两指针指向同一数组)
3. 顺序栈的初始化
顺序栈的初始化
1 2 3 4 5 6 7 8 9 InitStack (SqStack &S) {if (!S.base) exit (OVERFLOW); return OK;
4. 判断顺序栈是否为空
1 2 3 4 5 6 7 8 StackEmpty (SqStack S) {if (S.top==S.base)return TRUE;else return FALSE;
5. 求顺序栈的长度
1 2 3 int StackLength (SqStack S) {return S.top - S.base;
6. 清空、销毁顺序栈
1 2 3 4 5 ClearStack (SqStack &S) { if (S.base) S.top = S.base;return OK;
1 2 3 4 5 6 7 8 9 10 DestroyStack (SqStack &S) {if (S.base){0 ;NULL ;return OK;
7. 顺序栈的入栈
判断是否栈满,若满则出错(上溢)
元素e压入栈顶
栈顶指针加1
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 Push (SqStack &S, SElemType e) {if (S.top - S.base == S.Stacksize) return ERROR; return OK;realloc (S.base, (S.Stacksize+STACKINCREME) *sizeof (ElemType));if (!S.base) exit (OVERFLOW);
8. 顺序栈的出栈
判断是否栈空,若空则出错(下溢)
栈顶指针减1
获取栈顶元素e
1 2 3 4 5 6 7 8 9 Pop (SqStack &S, SElemType &e) {if (S.top==S.base) return ERROR; return OK;
9. ⭐小结
以下代码是在Vscode上实现的顺序栈的操作
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 #include <stdio.h> #include <stdlib.h> #define TRUE 1 #define FALSE 0 #define OK 1 #define ERROR 0 #define OVERFLOW -2 #define MAXSIZE 100 typedef int Status;typedef int SElemType; typedef struct {int stacksize; Status InitStack (SqStack &S) {new SElemType[MAXSIZE];if (!S.base) exit (OVERFLOW); return OK;Status StackEmpty (SqStack S) {if (S.top == S.base)return TRUE; else return FALSE; int StackLength (SqStack S) return S.top - S.base;Status ClearStack (SqStack &S) { if (S.base) S.top = S.base;return OK;Status DestroyStack (SqStack &S) {if (S.base){delete S.base;0 ;NULL ;return OK;Status Push (SqStack &S, SElemType e) {if (S.top - S.base == S.stacksize) return ERROR; return OK;Status Pop (SqStack &S, SElemType &e) {if (S.top==S.base) return ERROR; return OK;void PrintStack (SqStack S) if (!S.base) {printf ("当前栈不存在\n" );else if (StackEmpty (S)) {printf ("当前栈为空\n" );else {printf ("栈中的内容为:\n" );while (p != S.top) {printf ("%d " , *p);printf ("\n" );int main () printf ("----初始化一个栈----\n" );InitStack (S);printf ("----输出栈中的内容----\n" );PrintStack (S);printf ("\n----入栈操作----\n" );int e = 1 ;Push (S, e);2 ;Push (S, e);3 ;Push (S, e);8 ;Push (S, e);printf ("----输出栈中的内容----\n" );PrintStack (S);int length = StackLength (S);printf ("栈当前的长度为:%d\n" ,length);printf ("\n----出栈操作----\n" );while (!StackEmpty (S)) {0 ; Pop (S, e2);printf ("出栈元素:%d\n" , e2);printf ("栈已为空\n" );printf ("\n----清空栈----\n" );ClearStack (S);PrintStack (S);printf ("\n----销毁栈----\n" );DestroyStack (S);PrintStack (S);return 0 ;
3.3.3 链栈的表示和实现
链栈是运算受限的单链表,只能在链表头部进行操作
1 2 3 4 5 typedef struct StackNode {struct StackNode *next ;
链栈
链表的头指针就是栈顶
不需要头结点
基本不存在栈满的情况(内存中有空间就行)
空栈相当于头指针指向空
插入和删除仅在栈顶处执行
1. 链栈的初始化
1 2 3 4 5 void InitStack (LinkStack &S) {NULL ;return OK;
2. 判断链栈是否为空
1 2 3 4 Status StackEmpty (LinkStack S) {if (S==NULL ) return TRUE;else return FALSE;
3. 链栈的入栈
链栈的入栈
1 2 3 4 5 6 7 8 Status Push (LinkStack &S, SElemType e) {return OK;
4. 链栈的出栈
链栈的出栈
1 2 3 4 5 6 7 8 Status Pop (LinkStack &S,SElemType &e) {if (S==NULL ) return ERROR;return OK:
5. 取栈顶元素
1 2 3 SElemType GetTop (LinkStack S) {if (S!=NULL ) return S->data;
3.4 栈与递归
递归的定义
若一个对象部分地包含它自己,或用它自己给自己定义,则称这个对象是递归的
若一个过程直接地或间接地调用自己,则称这个过程是递归的过程
\(f(g(x))\)
3.5 队列的表示和操作实现
队列
3.5.1 队列抽象数据类型的定义
1703332636642
3.5.2 队列的顺序表示和实现
1. 队列的顺序表示
队列的物理存储可以用顺序存储结构,也可用链式存储结构。相应的,队列的存储方式也分为两种,即顺序队列和链式队列。
队列的顺序表示:用一维数组base[MAXQSIZE]
1 2 3 4 5 6 #define MAXQSIZE 100 typedef struct {int front; int rear;
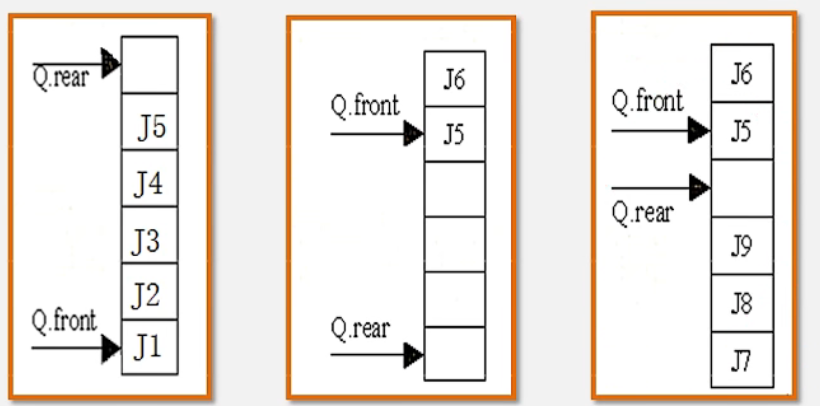
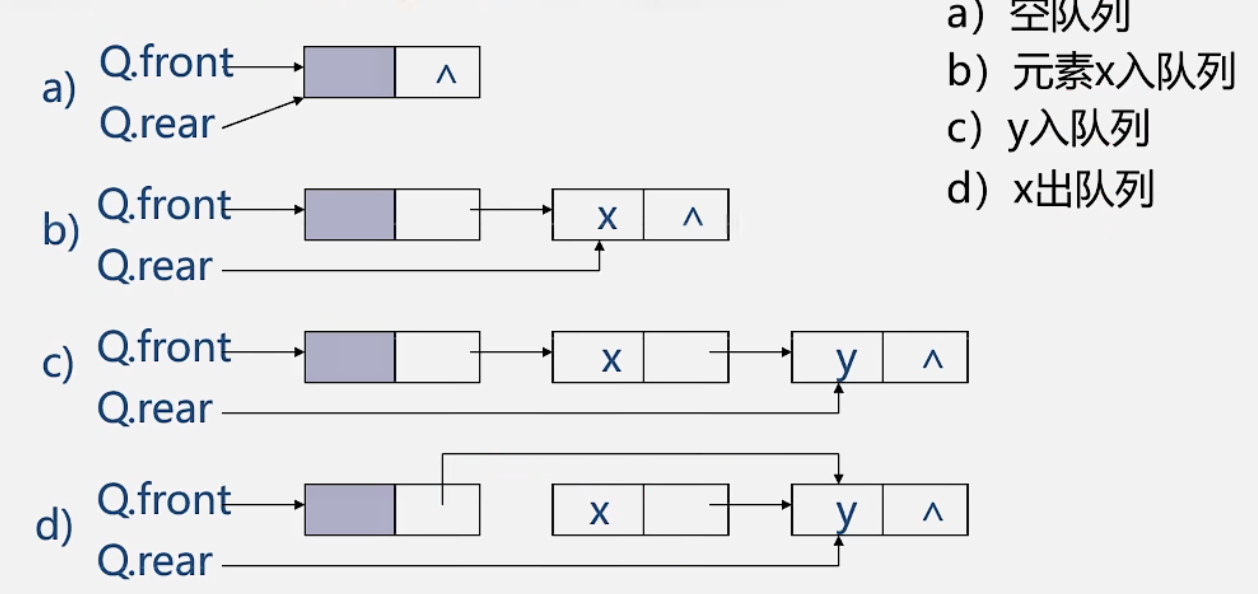
初始状态(队空条件):Q.front == Q.rear == 0。
进队操作:队不满时,先送值到队尾元素,再将队尾指针加1。
出队操作:队不空时,先取队头元素值,再将队头指针加1。
队列的操作
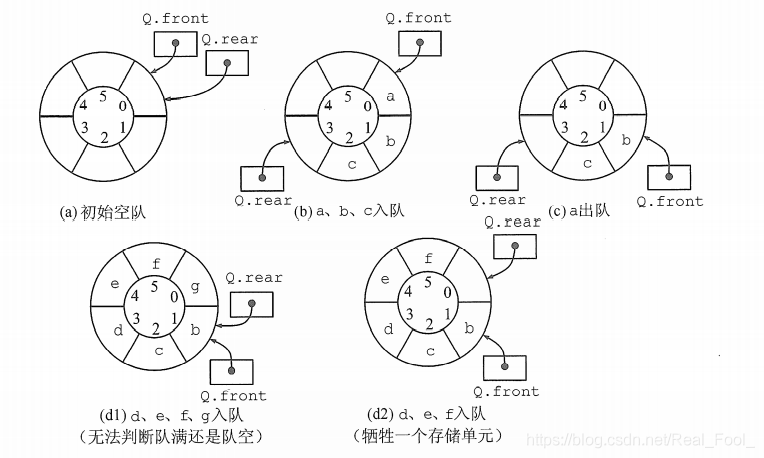
如图d,队列出现“上溢出”,然而却又不是真正的溢出,所以是一种“假溢出”。
解决假上溢的方法:
1、将队中元素依次向队头方向移动。缺点:浪费时间,每移动一次,队中元素都要移动
2、将队空间设想成一个循环 的表即分配给队列的m个存储单元可以循环使用,当rear为maxqsize时,若向量的开始端空着,又可从头使用空着的空间。当front为maxqsize时,,也是一样
怎么实现呢,想到了模运算,循环实现
3.5.3 循环队列
解决假上溢的方法——引入循环队列
base[0]接在base[MAXQSIZE -1]之后,若rear+1==M,则令rear=0
实现方法:利用模(mod,C语言中: %) 运算
插入元素
1 2 Q .[Q.rear ] =x;Q .Q .1 ) % MAXQSIZE;
删除元素
1 2 x = Q.base[Q.front]Q.front = (Q.front+1 ) % MAXQSIZE
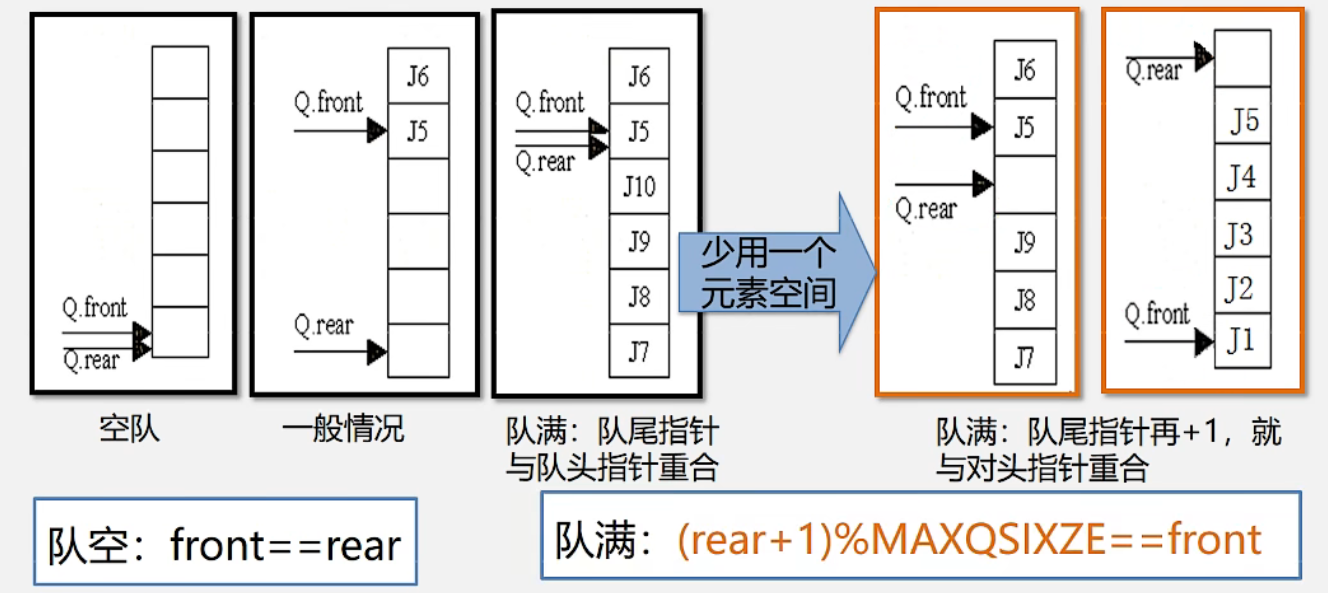
循环队列:循环使用为队列分配的存储空间。
循环队列
队空:front==rear 队满:front==rear
解决方案:
另外设一个标志以区别队空、队满
另设一个变量,记录元素个数
少用一个元素空间 (这里我们用这个
如何判断队空队满
1. 循环队列的类型定义
1 2 3 4 5 6 7 8 9 10 #define MAXQSIZE 100 typedef struct {int front; int rear;
2. 循环队列的初始化
1 2 3 4 5 6 7 8 9 10 11 12 InitQueue (SqQueue &Q) {if (!Q.base) exit (OVERFLOW);0 ; return OK;
1 2 3 4 5 6 7 8 9 10 11 InitQueue (SqQueue *Q) {0 ;0 ;return OK;
3. 求队列的长度
1 2 3 4 5 int QueueLength (SqQueue Q) {return (L);
求循环队列的长度
左间的图:rear是5,front是0,5-0+6=11,11%6=5
中间的图:rear是0,front是4,0-4+6=2,2%6=2
右边的图:rear是3,front是4,3-4+6=5,5%6=5
4. 循环队列入队
1 2 3 4 5 6 7 EnQueue (SqQueue &Q, QElemType e) {if ((Q.rear+1 ) % MAXQSIZE == Q.front) return ERROR; 1 ) % MAXQSIZE; return OK;
5. 循环队列出队
1 2 3 4 5 6 7 DeQueue (SqQueue &Q, QElemType &e) {if (Q.front == Q.rear) return ERROR;1 ) % MAXQSIZE; return OK;
6. 取队头元素
1 2 3 4 SElemType GetHead (SqQuere Q) { if (Q.front!=Q.rear) return Q.base[Q.front];
3.5.3 队列的链式表示和实现
若用户无法估计所用队列的长度,则宜采用链队列
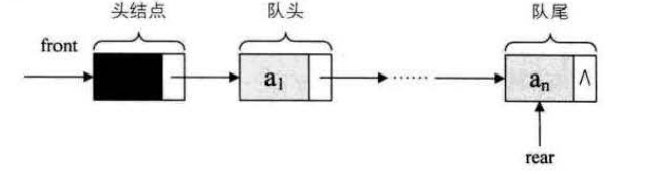
队列的链式存储结构表示为链队列,它实际上是一个同时带有队头指针和队尾指针的单链表,只不过它只能尾进头出而已。
链队列
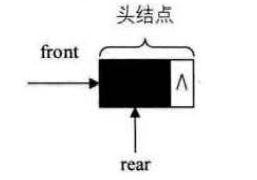
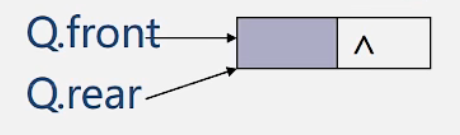
空队列时,front和real都指向头结点。
链队列为空时
1. 链队列的类型定义
1 2 3 4 5 6 7 8 9 10 11 #define MAXQSIZE 100 typedef struct Qnode {struct Qnode *next ;typedef struct {
链队列运算指针变化状况
2. 链队列初始化
链队列初始化
1 2 3 4 5 6 7 InitQueue (LinkQueue &Q) {malloc (sizeof (Qnode)); if (!Q.front) exit (OVERFLOW));NULL ;return OK;
解释一下Q.front = Q.rear = (QueuePtr)malloc(sizeof(Qnode));
这行代码的效果是创建了一个包含一个节点的链式队列,并将队列的前端和尾端指针都指向这个节点。
sizeof(Qnode):这里使用 sizeof 运算符来获取 Qnode
结构体的大小,单位是字节。sizeof(Qnode) 返回的是 Qnode
结构体所占用的内存大小。
malloc(sizeof(Qnode)):malloc
函数用于动态分配内存。它接受一个参数,即要分配的字节数,然后返回一个指向新分配内存区域起始位置的指针。在这里,malloc(sizeof(Qnode))
分配了足够大小的内存以容纳一个 Qnode
结构体,并返回一个指向这块内存的指针。
(QueuePtr):这是类型转换操作符,将前面 malloc 返回的指针转换为
QueuePtr 类型。这是为了保证类型匹配,因为 malloc 返回的是
void* 类型的指针,而 QueuePtr 是指向 struct Qnode
的指针类型。
Q.front = Q.rear = (QueuePtr)malloc(sizeof(Qnode));:这行代码将刚刚分配的内存地址赋给
Q.front 和
Q.rear。这两个指针都指向同一个新分配的节点,这也表示队列目前只有这一个节点。
这个节点的 data 成员和 next 成员的值在这个时候尚未初始化。
3. 销毁链队列
算法思想:从队头结点开始,依次释放所有结点
1 2 3 4 5 6 7 8 9 10 DestroyQueue (LinkQueue &Q) {while (Q.front){free (Q.front);return OK;
4. 链队列的入队
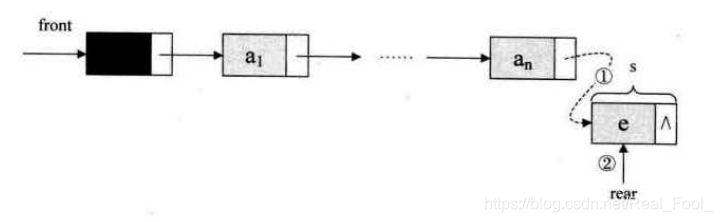
链队列的入队
1 2 3 4 5 6 7 8 9 10 11 Status EnQueue (LinkQueue &Q, QElemType e) {malloc (sizeof (Qnode));if (!p) exit (OVERFLOW);NULL ;return OK;
5. 链队列的出队
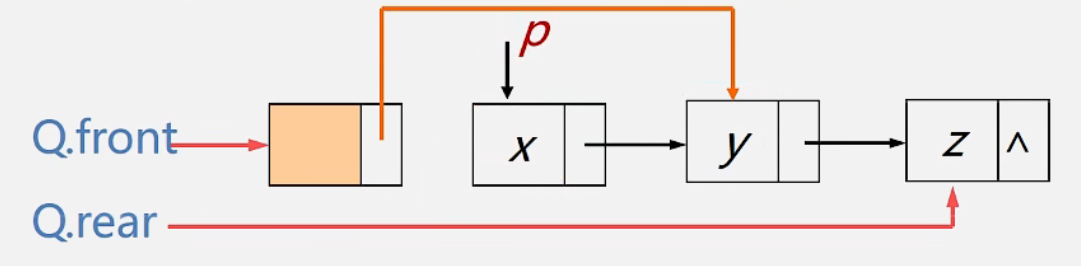
链队列的出队
1 2 3 4 5 6 7 8 9 10 11 12 13 DeQueue (LinkQueue &Q, QElemType &e) {if (Q.front= =Q.rear) return ERROR;if (Q.rear == P) Q.rear=Q.front;free (P); return OK;
6. 求链队列的队头元素
1 2 3 4 5 Status GetHead (LinkQueue Q QElemType &e) {if (Q.front==Qrear) return ERROR;return OK;
参考:
节点和结点有什么区别?
(baidu.com)
数据结构:栈和队列(Stack
& Queue)【详解】-CSDN博客