密码学-1-绪论
本文最后更新于:2024年4月3日 晚上
密码学的发展概况
密码学是一门古老、年轻且深奥的学科。
密码学经历了从古典密码学到现代密码学的演变。
密码学是研究信息系统安全保密的科学。它包括密码编码学和密码分析学。
1949年前密码技术是一门技术性很强的艺术,而不是一门科学。
1949年shannon “保密系统的通信理论”,密码学成为科学。
1976年Diffie和Hellman“密码学的新方向”,密码学的一场革命,标志着公钥密码学的出现
1977年美国国家标准局公布DES,并公开算法,揭开神秘面纱。
密码学的相关概念
密码学 (cryptology):是密码编码学和密码分析学的统称
密码编码学(cryptography):
- 通过变换消息使其保密的科学和艺术
- 是密码理论的基础,也是保密系统设计的基础
密码分析学(cryptanalysis):在未知密钥的情况下从密文推演出明文或密钥的艺术
密码编码学和密码分析学既相互对立,又相互促进和发展
明文
作为加密输入的原始信息,即消息的原始形式,通常用\(m\) (message) 或\(p\) (plaintext)表示。所有可能明文的有限集称为明文空间,通常用\(M\)或\(P\)表示。
密文
明文经加密变换后的结果,即消息被加密处理后的形式,通常用\(c\) (ciphertext)表示。所有可能密文的有限集称为密文空间,通常用\(C\)表示。
密钥
参与密码变换的参数,通常用\(k\)(key)表示,包括加密密钥\(k_{e}\)和解密秘钥\(k_d\)。一切可能密钥构成的有限集称为密钥空间,通常用\(K\)表示。
加密算法
将明文变换为密文的变换函数,相应的变换过程称为加密,即编码的过程。通常用\(E\) (Encryption)表示,即\(c=\) \(E_{k_e}(p)\)。
解密算法
将密文恢复为明文的变换函数,相应的变换过程称为解密,即解码的过程。通常用\(D\left(\mathrm{Decryption}\right)\)表示,即\(p=\) \(D_{k_d}(c)\)
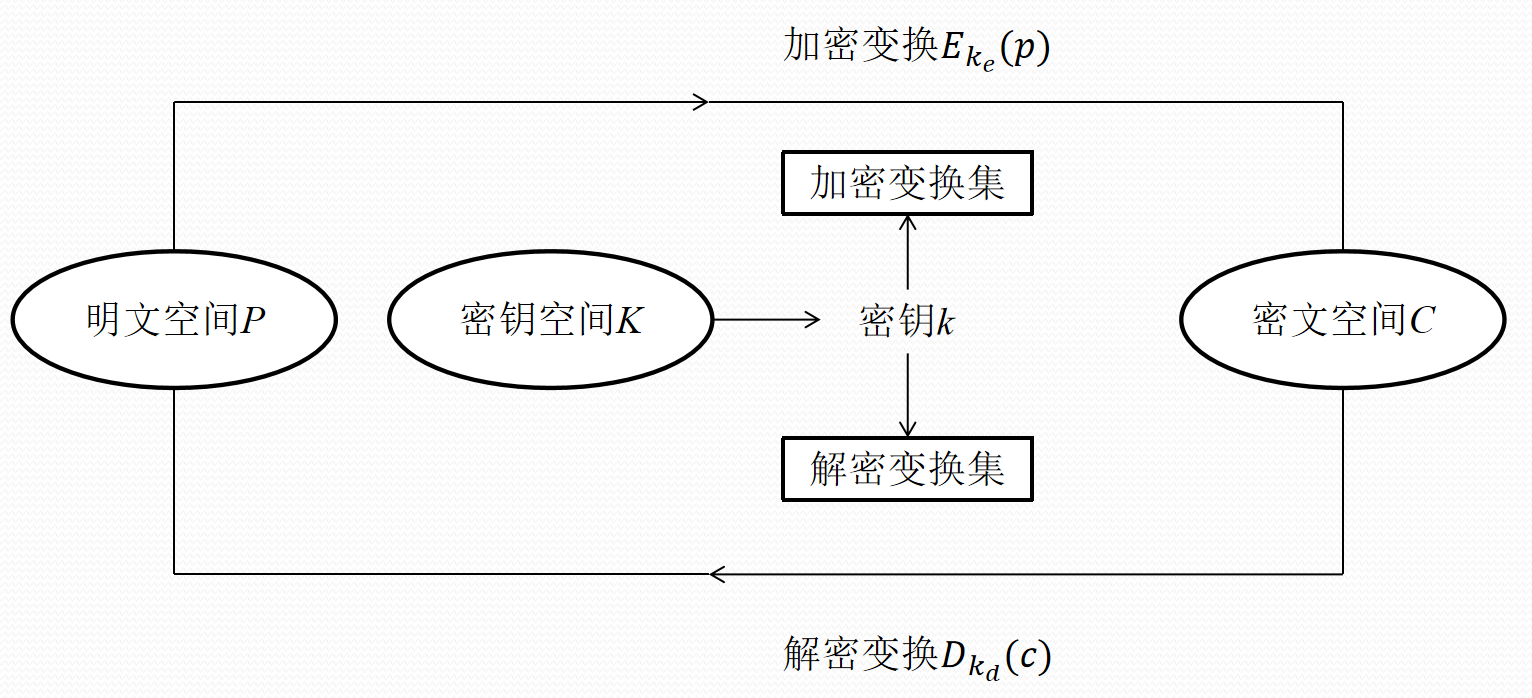
密码学中的五元组\(\{P,C,K,E,D\}\)
对于明文空间\(P\)中的每一个明文\(p\),加密算法\(E\)在加密密钥\(k_{e}\)的控制下将明文\(p\)加密成密文\(c\);而解密算法\(D\)则在解密密钥\(k_d\)的控制下将密文\(c\)解密成同一明文\(p\) , 即:
对\(\forall p\in P,(k_e,k_d)\in K\),有\(p=D_{k_d}(E_{k_e}(p))\)
密码体制的组成:
密码分析分类:
根据密码分析者对明文、密文等信息掌握的多少
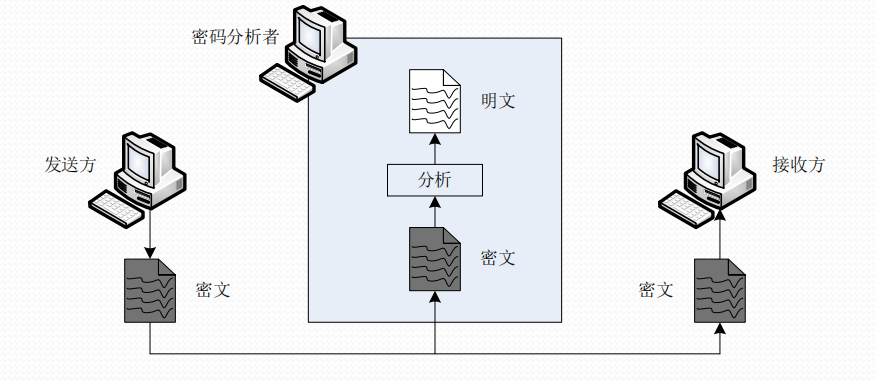
(1)唯密文攻击\((Ciphertext-only Attack)\):
- 密码分析者仅知道一些密文。
✓ 破译者已知:密码算法、待破译的密文
✓ 密码算法必须要能抵抗这类攻击,这是密码算法设计的最低要求
✓ 蛮力攻击 \((Brute-force Attack)\):密码分析者测试所有可能的密钥来解密截获的密文,直到得到的明文看起来有意义。要对付这类攻击,可能的密钥数必须足够多。
✓ 统计攻击 \((Statistical Attack)\):密码分析者分析明文语言的某些固有的内在属性(即统计特征),从而获得某种好处或利益。要对付这类攻击,密码算法必须要能隐藏明文语言的统计特征。
✓ 模式攻击 \((Pattern Attack)\):密码分析者利用密文中形成的某些模式来实施攻击。要对付这类攻击,要求加密所得到的密文尽可能看起来像是随机的
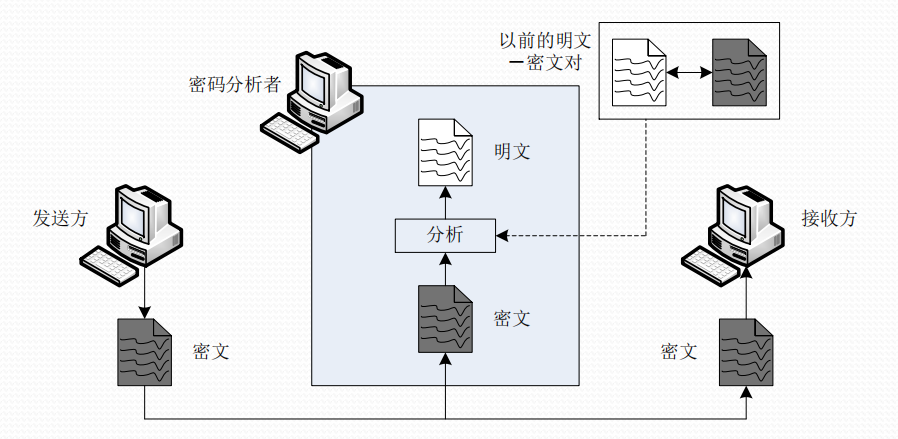
(2)已知明文攻击\((Known-plaintext Attack)\):
- 密码分析者知道一些明文和相应的密文。(随便给的一些明文和密文)
✓ 破译者已知:密码算法、一定数量的明文-密文对、截获的待解密的密文
✓ 可通过更改密钥来抵御该种攻击
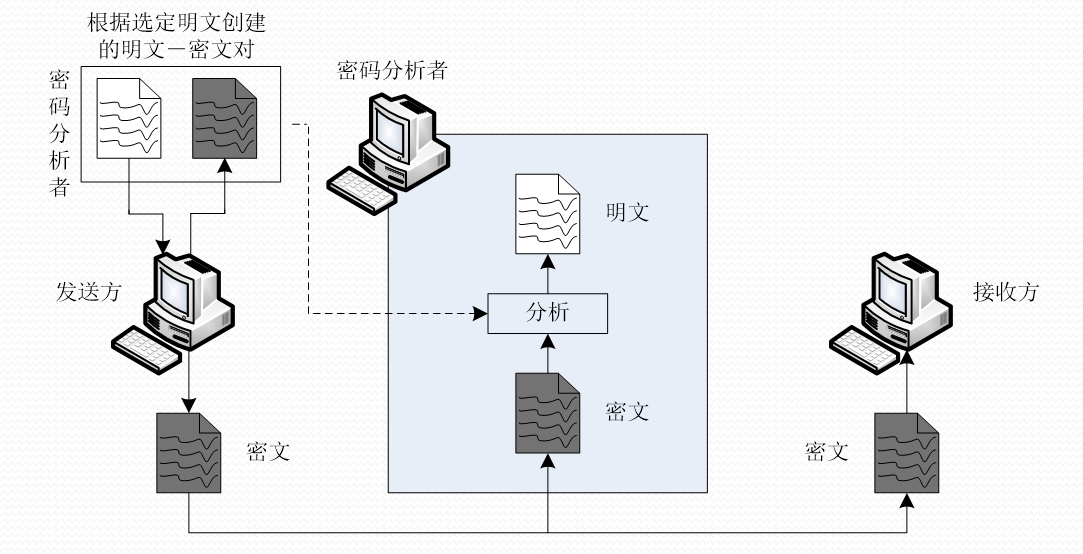
(3)选择明文攻击 \((Chosen-plaintext Attack)\):
- 密码分析者可以选择一些明文,并得到相应的密文。(有加密机)
✓ 破译者已知:密码算法、选定的明文和对应的密文
✓ 在密码分析者能够访问到发送方的计算机时可能发生
(4)选择密文攻击\((Chosen-ciphertext Attack)\):
- 密码分析者可以选择一些密文,并得到相应的明文。(有解密机)
✓ 破译者已知:密码算法、选定的密文和对应的明文
✓ 在密码分析者能够访问到接收方计算机时可能发生
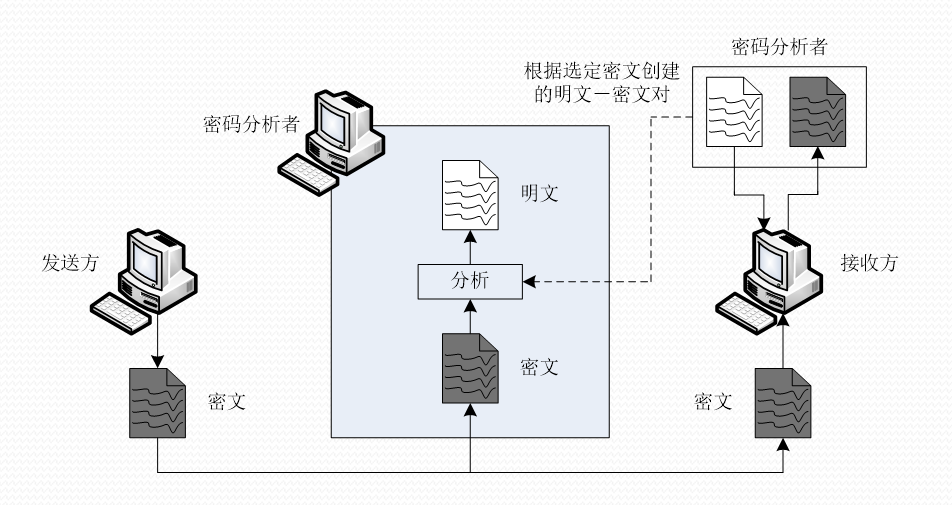
(5)选择文本攻击\((Chosen-text Attack)\):
✓ 破译者已知:密码算法、选定的明文和对应的密文、选定的密文和对应的明文
✓ 选择明文攻击和选择密文攻击的结合
总结:
唯密文攻击是最困难的
上述攻击的强度是递增的
一个密码体制是安全的,通常是指在前三种攻击下的安全性
唯密文攻击的强度最弱,攻击强度依此增加。
公钥加密中选择明文攻击是自动发生的,因为是公钥加密,密钥是公开的🐕
无条件安全的(不可破译的):一次一密方案(一次一密乱码本),不可破译的
计算上安全的:流密码、分组密码、公钥密码,给你无限的资源你是可以破译的,这样我们也是可以接受的
密码算法只要满足以下两条准则之一就行:
(1) 破译密文的代价超过被加密信息的价值。
(2 ) 破译密文所花的时间超过信息的有用期。
满足以上两个准则的密码算法在实际中是可用的。
古典密码
代替密码
代替密码是指先建立一个替换表,加密时将需要加密的明文依次通过查表,替换为相应的字符。明文字符被逐个替换后,生成无任何意义的字符串,即密文。代替密码的密钥就是其替换表。
根据密码算法加解密时使用替换表多少的不同,代替密码又可分为单表代替密码和多表代替密码。
✓单表代替密码:密码算法加解密时使用一个固定的替换表
✓多表代替密码:密码算法加解密时使用多个替换表
单表代替密码
- 移位密码
明文空间\(P\)、密文空间\(C\)和密钥空间\(K\)满足\(P=C=K=\{0,1,2,...,25\}=\mathbb{Z}_{26}\)
即把26个英文字母与整数0,1, 2, ...,25一一对应
注意这里A对应的是0,不是1哦😋


- 使用密钥的单表代替加密
选用一个英文短语或者单词串作为密钥,去掉其中重复的字母得到一个无重复字母的字母串,然后将字母表中的其他字母依次写于此字母串之后,就可构造出一个字母代替表
✓ 对于明文为英文单词或短语的情况时,密钥短语密码最多可能有\(26!=4×1026\)个不同的替换表。

- 仿射密码 (Affine cipher)
✓ 仿射密码是一种线性变换。仿射密码的明文空间和密文空间与移位密码相同,但密钥空间为 \(K{=}\{(k_1,k_2)|k_1,k_2\in\mathbb{Z}_{26}\), \(\gcd(k_1,26){=1}\)
✓ 对任意\(p{\in}P,\quad c{\in}C,\quad k{=}(k_1,k_2){\in}K\),
定义加密变换为: \(c=E_k\left(p\right)=k_1p+k_2\left({\mathrm{mod}}26\right)\)
相应解密变换为:\(p=D_k\) \((c)=k_1^{-1}\left(c-k_2\right)({\mathrm{mod}}26)\)。其中,\(k_1k_1^{-1}=1\pmod{26}\)。
✓ 要求\((k_1,26)=1\) , 否则就会有多个明文字母对应一个密文字母的情况
✓ 密钥空间大小为\((k_1,k_2)\)=12×26=312, 因为与26互素的\(k_{1}\)有12个取值,\(k_{2}\)有26个取值
\[ \begin{aligned} &\text{设明文消息为China,密钥}k=(k_1,k_2)=(7,3)\text{,用仿射密码对其进行加密,然后再进行解密。} \\ &\text{解答:利用扩展的欧几里德算法可计算出}k_1^{-1}=7^{-1}=15 \mathrm({mod~}26) \\ &\text{加密函数为}E_k(p)=7*p+3\mathrm{~(mod~}26)\text{,对应}\text{的解密函数为}D_k\left(c\right)=15*(c-3)(mod 26)=15c-19 ({\mathrm{mod}26)。} \end{aligned} \]
明文消息China对应的数字序列为(2,7,8,13,0),用仿射密码对明文进行加密:
\[c=E_k(p)=7\times\begin{bmatrix}2\\7\\8\\13\\0\end{bmatrix}+\begin{bmatrix}3\\3\\3\\3\\3\end{bmatrix}=\begin{bmatrix}17\\52\\59\\94\\3\end{bmatrix}\mathrm{mod}26=\begin{bmatrix}17\\0\\7\\16\\3\end{bmatrix}=\begin{bmatrix}R\\A\\H\\Q\\D\end{bmatrix}\]
密文消息为RAHQD
解密:
\[D_k(c)=15\times\begin{bmatrix}17\\0\\7\\16\\3\end{bmatrix}-\begin{bmatrix}19\\19\\19\\19\\19\end{bmatrix}=\begin{bmatrix}236\\-19\\86\\221\\226\end{bmatrix}\mathrm{mod}26=\begin{bmatrix}2\\7\\8\\13\\0\end{bmatrix}=\begin{bmatrix}C\\H\\I\\N\\A\end{bmatrix}\]
单表代替密码特点:
✓ 密钥量很小,不能抵抗穷尽搜索攻击
✓ 没有将明文字母出现的概率掩藏起来,很容易受到统计分析的攻击
多表代换密码
- 使用从明文字母到密文字母的多个映射来隐藏单字母出现的频率分布
- 每个映射是单表代替密码中的一对一映射
- 将明文字母划分为长度相同的消息单元,称为明文分组,对明文字母成组地进行代替
- 特点:使用两个或两个以上的替换表
普莱费尔密码(Playfair Cipher)
维吉尼亚密码(Vigenere Cipher)
希尔密码(Hill Cipher)
\(Playfair\)密码
✓ 将明文中的双字母作为一个单元对待,并将这些单元转换为密文字母组合
✓ 基于一个5×5字母矩阵,使用一个关键词(密钥)来构造
✓ 构造方法:从左至右,从上至下依次填入关键词的字母(去除重复的字母),然后再以字母表顺序依次填入其他的字母。加密时字母I和J被算作一个字母


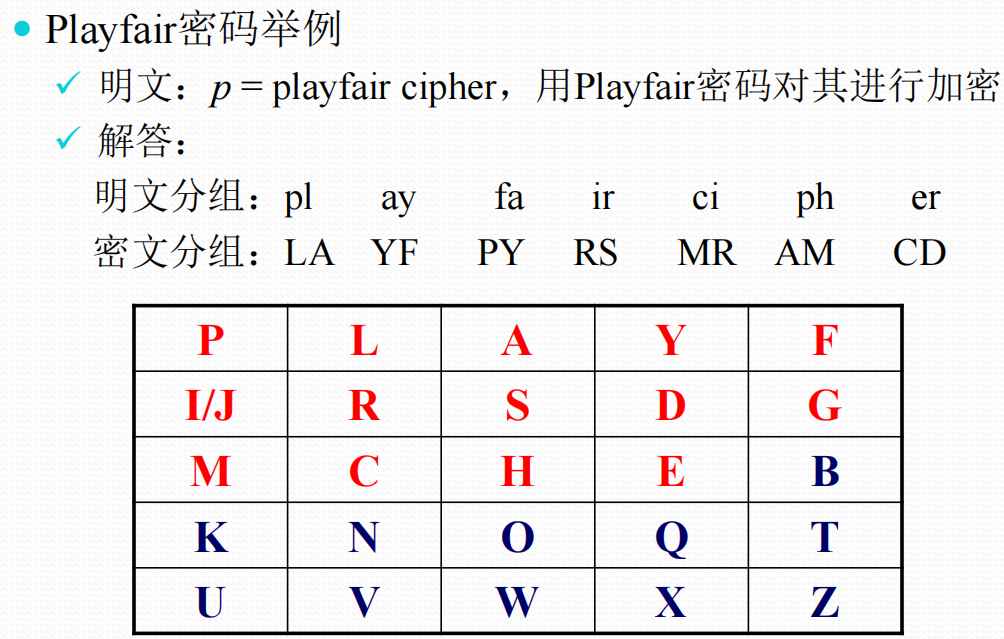
Playfair密码的特点
✓ 虽然仅有26个字母,但有26×26=676种双字母组合。因此识别各种双字母组合要困难得多
✓ 各个字母组的频率要比单字母呈现出大得多的范围,使得频率分析困难得多
✓ 仍然使许多明文语言的结构保存完好,使得密码分析者能够利用
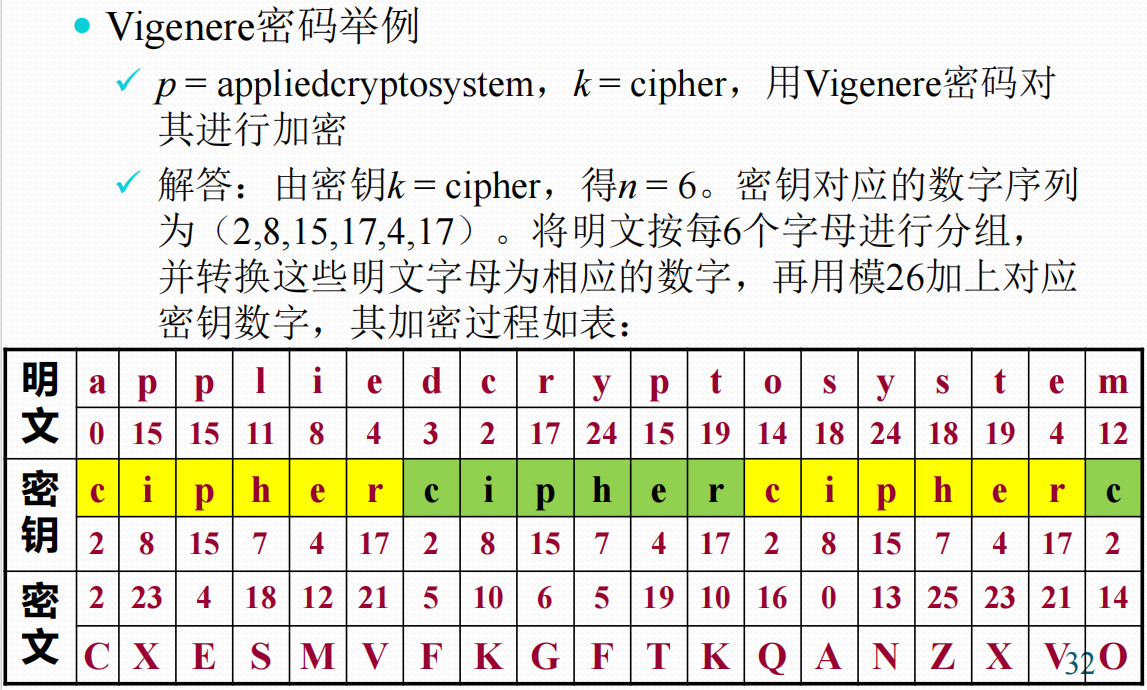
\(Vigenere\)密码
✓ 最著名的多表代替密码的例子
✓ 使用一个词组作为密钥,密钥中每一个字母用来确定一个代替表,每一个密钥字母用来加密一个明文字母,等所有密钥字母使用完后,密钥又再循环使用
✓ 该密码体制有一个参数n。在加解密时,同样把英文字母映射为0-25的数字再进行运算,并按n个字母一组进行变换。
设密钥\(k=(k_1,k_2,...,k_d)\),明文\(p=(p_1,p_2,...,p_n)\),密文\(c=(c_1,c_2,\cdotp\cdotp\cdotp,c_n)\)
加密变换:\(E_k(p)=(c_1,c_2,\cdotp\cdotp\cdotp,c_n)\),其中\(c_i=(p_i+k_i)({\mathrm{mod}}26), i=1,2,……n\)
解密变换:\(D_k(c)=(p_1,p_2,...,p_n)\),其中\(p_i=(c_i-k_i)({\mathrm{mod}}26),\:i=1,2\cdots,n\)
\(Hill\)密码
单表代替密码攻击
多表代替密码的破解
多表代替密码从一定程度上隐藏了明文消息的一些统计特征,破译相对较为困难
在多表代替密码的分析中,首先要确定密钥的长度,也就是要确定所使用的加密表的个数,然后再分析确定具体密钥
确定密钥长度的常用方法两种,即Kasiski测试法(Kasiski test)和重合指数法(index of coincidence)
破译思路:设法找出密钥长度,将多表替换→单表替换,再破译单表替换密码。
Kasiski测试法
➢ 原理
若用给定的n个密钥表周期性地对明文字母加密,则当明文中有两个相同字母组在明文序列中间隔的字母数为n的倍数时,这两个明文字母组对应的密文字母组必相同。但反过来,若密文中出现两个相同的字母组,它们所对应的明文字母组未必相同,但相同的可能性很大
➢ Kasiski的测试过程
搜索长度至少为2的相同密文段,记录这些相同密文段到起始点之间的距离;假设得到如下几个距离X1,X2,…,那么密钥长度n可能就是这些距离的最大公因子
Kasiski测试法举例
明文:requests additional test
密钥:TELEXTEL EXTELEXTEL EXTE
密文:CAVKTBLT EUQWSWJGEA LTBL
密文包含字母序列TBL两次,间隔距离为15。密钥的实际长度为5,因此相同字母组的距离反映了密钥长度n的相关信息。
若公因子不唯一,则采用后续的重合指数法确定密码长度
重合指数法
如果考虑来自26个字母表的完全随机文本,则每个字母都以相同的概率1/26出现,假定另一个随机文本放在第一个的下面,在上下位置出现相同字母\(a\)的概率为 (1/26)^2, 在两个随机文本的上下位置找到任意两个相同字母总的概率为 \(26*(1/26)^{2}=1/26=0.0385\) 。
但实际上,由于英文字母出现的概率是不同的,设字母\(a,b,c,\ldots z\)出现的概率分别为\(p_0,p_1,p_2,...,p_{25}\), 这样找到两个相同字母的概率为\(\sum_{i=0}^{25}p_i^2=0.065\)
定义:
设一个语言由\(n\)个字母构成,每个字母出现的概率\(p_i,1\leq i\leq n\),则重合指数是指其中两个随机元素相同的概率,记为
\[ I_c=\sum_{i=1}^np_i^2 \]
这样对于一个完全随机的文本\(I_C=0.0385\),与一个有意义的英语文本\(I_C=0.065\),差异是比较明显的。
重合指数的特点:单表代换密码中,密文的重合指数和明文相同。
重合指数法确定密钥长度
分析原理
假设密文串为\(Y=y_1y_2..y_n\),m是密钥字长度,将Y分割成m个子串
\(\mathrm{Y_1=y_1y_{1+m}y_{1+2m\cdots}}\)
\(\mathrm{Y_2=y_2y_{2+m}y_{2+2m\cdots}}\)
……
\(\mathrm{Y_m=y_{m}y_{2m}y_{3m\cdots}}\)
对于每个\(Y_i\), 其密文采用的是单表代换方法 (相同的密文对应相同的明文),其重合指数\(I_C({Y}_i)\)应接近0.065
通过尝试不同的m,找到重合指数最接近0.065的那个
Vigenere密码分析举例
经Vigenere密码加密后的密文为
CHREEVOAHMAERATBIAXXWTNXBEEOPHBSBQMQEQERBWRVXUOAKXAOSXXWEAHBWGJMMQMNKGRFVGXWTRZXWIAKLXFPSKAUTEMNDCMGTSXMXBTUIADNGMGPSRELXNJELXVRVPRTULHDNQWTWDTYGBPHXTFALJHASVBFXNGLLCHRZBWELEKMSJIKNBHWRJGNMGJSGLXFEYPHAGNRBIEQJTAMRVLCRREMNDGLXRRIMGNSNRWCHRQHAEYEVTAQEBBIPEEWEVKAKOEWADREMXMTBHHCHRTKDNVRZCHRCLQOHPWQAIIWXNRMGWOIIFKEE
Kasiski测试法分析
➢ 密文串CHR出现在1,166,236,276,286这几个位置,它们之间距离分别是165,70,40,10,这些距离只有一个公因子5,故猜测密钥字长度为5
重合指数法分析
➢ 尝试不同的密钥字长度,计算密文的重合指数
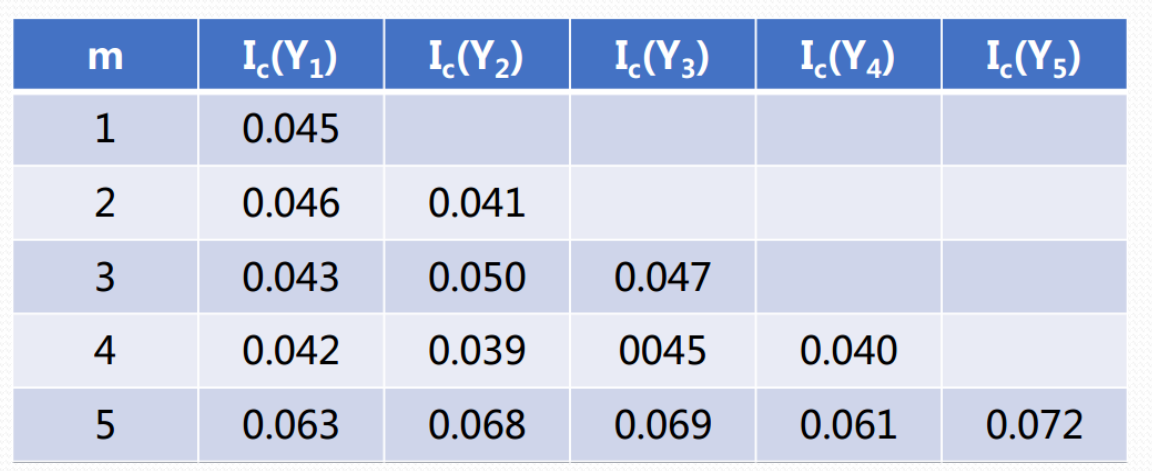
✓ 分析密钥字
➢ 确定密钥字长度后,可以使用频率分析方法分别解密Y1 , Y2 , ..., Ym
➢ Y1=CVABWEBQBUAWWQRWWXANTBDPXXRDWBFAXCWMNJJFAIACNRNCATBWKDMCDCQQXWK
➢ Y2=HOEITESEWOOEGMFTIFUDSTNSNVTNDPASNHESBGSEGEMRDRSHEAIEORTHNHOANOE
➢ Y3=RARANOBQRASAJNVRAPTCXUGRJRUQTHLVGRLJHNGYNQRRGINRYQPVEEBRVRHIRIE
➢ Y4=EHAXXPQEVKXHMKGZKSEMMIMEEVLWYXJBLZEIWMLPRJVELMRQEEEKWMHTRCPIMI
➢ Y5=EMTXBHMRXXXBMGXXLKMGXAGLLPHTGTHFLBKKRGXHBTLMXGWHVBEAAXHKZLWWGF
✓ 分析密钥字方法
对每一个\(\mathrm{Y_i}\), 猜测不同的\(k_i\)值,计算: \[ M_g=\sum_{i=0}^{25}p_i\frac{f_{i+g}}{n^{\prime}} \]
其中\(p_0,p_1,. .p_{25}\)是字母\(\mathrm{a, b, ..., z}\)在英文中出现的概率
其中\(\mathrm{f_0, f_1, ..f_{25}}\)是字母A,B,...,Z在密文中出现的次数
\(n^{\prime}\)是\(\mathrm{Y_i}\)的长度(即n/m)
当\(\mathrm{g= k_i}\)时,\(\mathrm{p_i} \approx \mathrm{f_{i+ g}/n^{\prime}, M_g}\approx 0.065\)
➢ 对每一个\(\mathrm{Y_i}\)中字母的频率进行统计,记为\(\mathrm{F_i} , \mathrm{~i= 1, 2, \ldots , k, }\),\(F_i\)中包含26个0~1的数值,分别对应每个字母的出现频率
➢ 用\(V_{0}\)表示26个英文字母各自的出现频率,即\(\mathrm{V}_0=[0.082, 0.015,\ldots,0.020,0.001]\), 将\(\mathrm{V}_{0}\)循环右移j位得到\(V_{\mathrm{j}}\), \(\mathrm{j= }0, 1, \ldots , 25\)
➢ 针对每个\(\mathrm{F_i}\),进行点乘计算\(\mathrm{F_i} \cdot \mathrm{V_j}\)
➢ 找出其中最大数值对应的j值,该值即为第i位密钥中的英文字母
所获得的密文长度越长,统计分析攻击的破译正确率越高
✓ 建立Mg分析表

✓ 分析结果
➢\(k_1=9,k_2=0,k_3=13,k_4=4,k_5=19, 对应密钥串为K=JANET\)
➢ 明文为
The almond tree was in tentative blossom. The days were longer, often ending with magnificent evenings of corrugated pink skies. The hunting season was over, with hounds and guns put away for six months. The vineyards were busy again as the well-organized farmers treated their wines and the more lackadaisical neighbors hurried to do the pruning they should have done in November.
重合指数法的应用
✓ 如果密文的重合指数较低,那么就可能是多表替代密码。维吉尼亚密码将密文分行,每行是单表替代密码。
✓ 在单表替代时,明文的字母被其它字母代替,但不影响文本的统计属性,即加密后密文的重合指数仍不变,CI(明文)= CI(密文),由此可以判断文本是用单表还是用多表替代加密的。
✓ 如果密钥长度(即密文分行的列数)正确,同一行密文有相同字母的概率接近0.065;如果密钥长度不对,则概率将大大小于0.065,显得更随机,由此得到密钥长度(可与Kasiski测试的结果对比)。
✓ 重合指数的估算能用于分析两个不同密文,比如接收到两段文本C1,C2,如果它们用同样的方式加密,则CI(C1)≈CI(C2)。
下面是一个公式喵: \[ \begin{align} &1\\ &\\ &\\ &\\ &\\ &\\ \end{align} \]