密码学-3-分组密码

本文最后更新于：2024年5月16日 早上

分组密码

概念

若明文流被分割成等长串，各串用相同的加密算法和相同的密钥进行加密，就是分组密码。即当：

  1. 明文和密文是固定长度为 \(\mathrm{n}\) 的比特串 \(m=m_1 m_2 m_3 \cdots m_n\), \(c=c_1 c_2 c_3 \cdots c_n\)

  2. 加密密钥和解密密钥相等，是固定长度为 \(r\) 的比特串 \(k=k_1 k_2 k_3 \cdots k_r\)

  3. 加密算法为 \(c=\operatorname{Enc}_K(m)\)

  4. 解密算法为 \(m=\operatorname{Dec}_k(c)=\operatorname{Dec}_K\left(\operatorname{Enc}_k(m)\right)\).

则称这样的加解密算法为分组密码

构造原则

分组密码的构造都应遵循下列几个原则：

  • 要有足够大分组长度（保证足够大的明文空间，避免给攻击者提供太多的明文统计特征信息）

  • 密钥空间要尽可能大（防止穷举密钥）

  • 保证足够强的密码算法复杂度以加强分组密码算法自身的安全性，

    方法如下：

    • 先将一个明文分组划分为若干子组分别进行处理，然后合并起来再做一些适当的变换，以增大密码算法强度。采取这样的措施也便于密码算法的实际分析和评测

    • 采用乘积密码的思想。通过两种或两种以上简单密码的逐次应用，构成强度比其中任何一个更强的加密结果。有效克服单一密码变换的弱点

  • 软件实现尽量采用子块和简单运算，采用加法、乘法、异或和移位等指令，易于标准处理器完成运算

  • 加解密硬件结构最好一致，这样便于应用超大规模集成芯片实现。以简化系统整体结构的复杂性。

增强密码算法复杂度的方法

在分组密码算法的安全策略中，用的最多的就是采用代换一置换网络(Substitution-Permutation Network)，简称SP网络

由多重S (substitution)变换和P (permutation)变换组合成的变换网络，即迭代密码，它是乘积密码的一种，由Shannon提出

S变换称为S盒，P变换称为P盒。S盒起到混乱作用，P盒起到扩散作用

substitution：代替，

permutation：[数] 排列；[数] 置换

  • S变换：把输入的一个n长的比特串转化为另一个m长的比特串输出（起到混乱的效果）
  • P盒变换: 通过把一个比特串中各比特的位置次序重新排列而得到新的比特串的变换（起到扩散的效果）
SP网络
SP

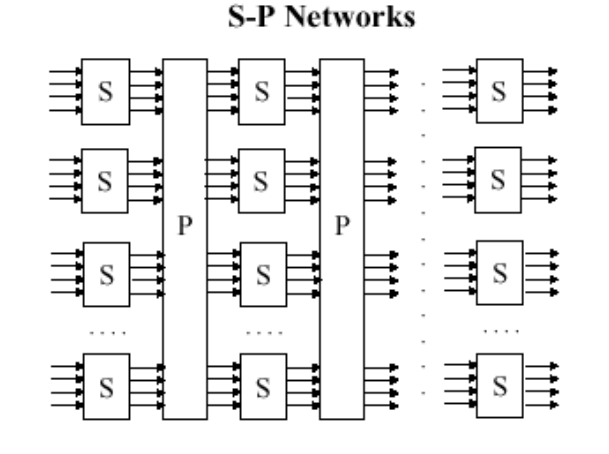
✓ S 盒的输入和输出位数不一定相同，有可逆和不可逆之分。可逆的S盒的输入位数和输出位数相同

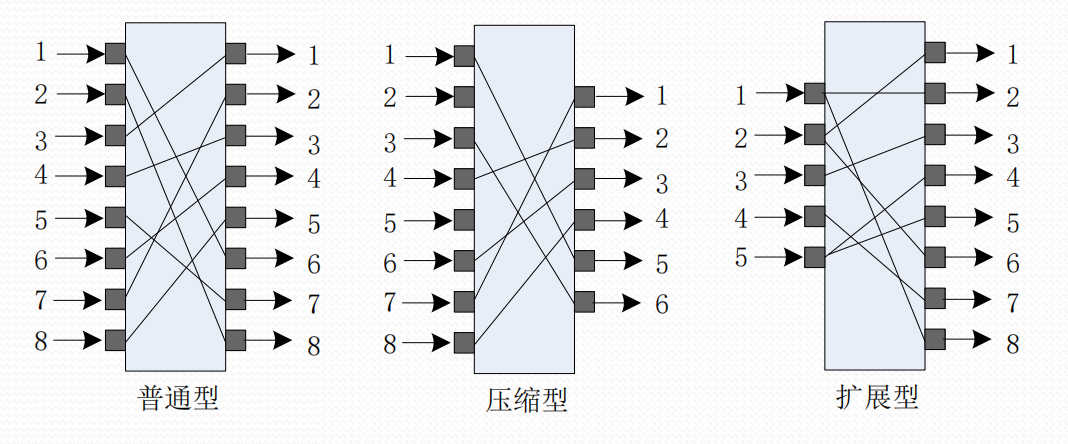
✓P盒有三种类型：

P盒

分组密码加密原理

分组密码一般都采用代换置换网络的结构，这种结构的一个典型代表是Feistel密码结构

基本思路是采用扩散与混乱两个主要思想：

  • 混乱：是指明文与密钥、以及密文之间的统计关系尽可能复杂化，使破译者无法理出相互间的依赖关系，从而加强隐蔽性。采用复杂的非线性代替变化（比如S盒单元）就可达到比较好的混乱效果。基于代替操作实现
  • 扩散：是指让明文中的每一位（包括密钥的每一位）直接或间接影响输出密文中的许多位，或者让密文中的每一位受制于输入明文以及密钥中的若干位，以便达到隐蔽明文的统计特性。它强调输入位只要很小变化，经过多轮变换后将导致输出发生多位变化，即明文的每位比特变化将引起密文许多比特位迅速发生改变。基于换位操作实现

乘积密码有助于实现扩散和混乱

✓ 顺序地执行两个或多个基本密码系统，使得最后结果的密码强度高于每个基本密码系统产生的结果（Feistel分组密码结构）

Lucifer算法

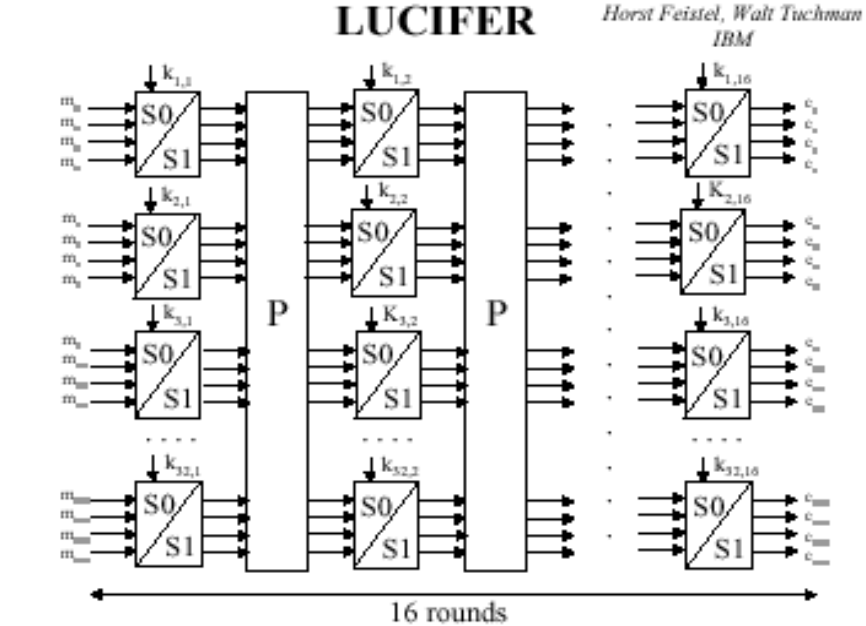
Lucifer算法是由IBM的德裔物理学家和密码学家霍斯特·费斯妥（Horst Feistel）在70年代中期设计的一种分组算法，它具有可变的轮数及可变的分组长度的特点，加密和解密过程互为逆运算。这个算法也被认为是DES的基础。

✓ 是用S盒和P盒交替在密钥控制下组成复杂的、分组长度足够大的密码设计方法

✓ 输入：128位明文和512位密钥

✓ 每个S盒的输入、输出均为4位，每轮32个S盒

✓ S盒的第一轮输入为明文，输出作为P盒的输入，经P盒换位后，再作为下一轮S盒的输入

✓ P盒是线性的，其作用是打乱各S盒输出数字的次序，将各S盒的输出分到下一级不同的各S盒的输入端，起到扩散作用

✓ S盒提供非线性变换，将来自上一级不同的S盒的输出进行”混淆“

Lucifer算法

现代分组密码都属于乘积密码，可分为两种类型：

✓ 同时使用了可逆和不可逆的基本变换部件，这一类被称为Feistel密码，DES是这一类的典型密码算法

✓ 只使用了可逆的基本变换部件，这一类被称为非Feistel密码，AES是这一类的典型密码算法

Feistel密码结构

  • 20世纪60年代未由IBM公司的Horst Feistel和Walter Tuchman在设计LUCIFFER分组密码算法（即DES前期模型）时提出
  • 特点：通过代替和置换（S-P网络）交替的方式来构造分组密码，其实就是基于混乱和扩散原理实现加解密运算

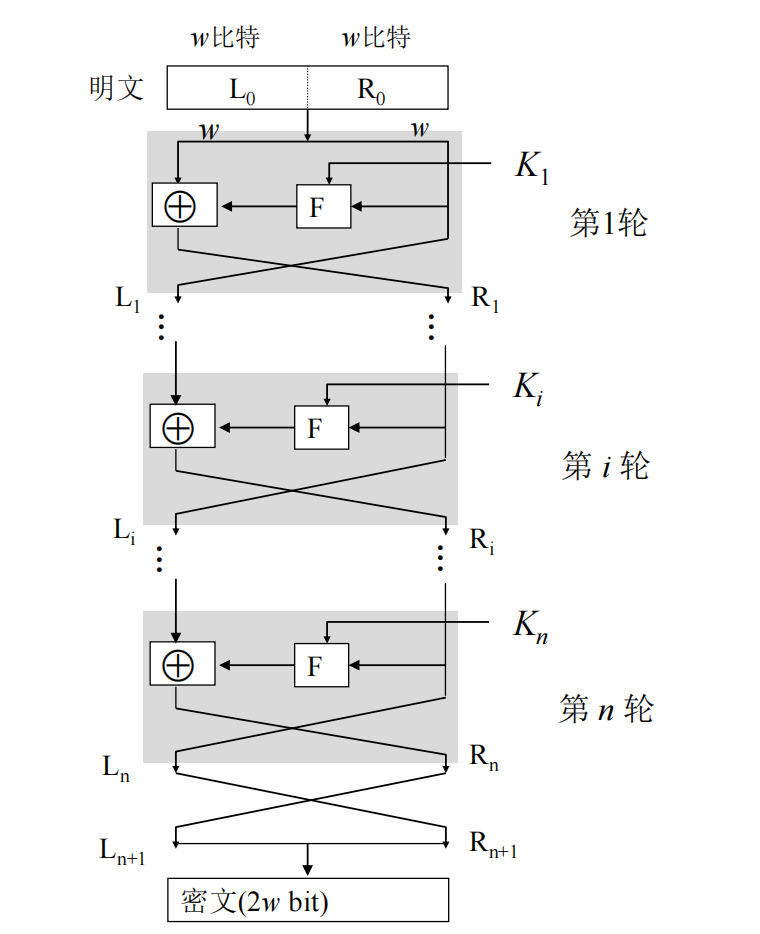
✓ 输入为2w比特的分组（称为左半分组\(L_0\)和右半分组\(R_0\)）

✓ Feistel网络由n个基本结构单元构成（但子密钥\(K_i\)互不相同），左右分组经过n轮迭代后交换位置组合在一起成为密文

✓ 运算逻辑关系 \[ \begin{aligned}&L_i=R_{i-1}(i=1,2,...,n)\\&R_i=L_{i-1}\oplus F(R_{i-1},K_i)(i=1,2,...,n)\end{aligned} \] ✓ 函数\(F\)称为轮函数

✓ \(K_i\)是第\(i\)轮用的子密钥，由加密密钥\(K\)生成

\(\checkmark\)每轮迭代结构相同

\(\checkmark\)每轮中右半数据被作用于轮函数F后，再与左半数据进行异或运算，即代替过程

\(\checkmark\)每轮迭代的轮函数相同，但每轮的子密钥\(K_i\)不同

\(\checkmark\)代替过程完成后，再交换左右两半数据实现置换

Feistel密码结构

Feistel结构实现依赖的主要参数与特征

分组长度：越长安全性越高，但运算速度越慢，一般选用64、128、256或512位的分组长度

密钥长度：越长安全性越高，但运算速度越慢，通常使用的密钥长度为128、256、512位等

迭代轮数：越多安全性越高，但运算开销越大，通常采用16次

子密钥生成算法：算法越复杂，密码分析越困难

轮函数F：复杂性越高，密码分析越困难

Feistel结构的解密过程本质上与加密过程一致，基本处理方法是：以密文作为算法的输入，并按加密的逆序使用子密钥\(K_i\)

Feistel密码举例

Feistel密码举例

用Feistel密码加密8-bit的明文\(P=DF\)（十六进制表示），密钥\(K=ABC\)（十六进制表示）

运算过程
运算过程2

分组密码设计准则

需要重点考虑

  • S盒的设计
  • P盒的设计
  • 轮函数F的设计
  • 迭代轮数
  • 密钥扩展算法

S盒和P盒的设计准则

分组密码中的S-P网络，是一个集掩蔽、混淆、扩散于一体的综合性部件，目的就是实现高度的非线性化和良好的雪崩效应

  • S盒：分组密码的非线性部分的核心部件，起着加密算法的混淆作用，直接影响整个分组密码算法的安全强度
    • 非线性度：目前有的采用群加密运算乘法 \(mod\ 2^n+ 1\)（如IDEA）或利用非素数域\(GF(2^n)\)上的幂函数（如AES）来构造S盒，以增强高度非线性度变换
    • 分均匀性：抵抗差分密码分析的能力要强
    • 可逆性完整、没有”陷门“
    • 不宜过大，否则会增加设计困难度和算法存储量
  • P盒：由于P盒多半是继若千个S盒部件之后，因此，P盒的设计准则就是要实现良好的雪崩效应，进一步增加扩散程度，比如DES中要求1比特输入希望能引起大约一半输出位的快速变化响应

雪崩效应：

✓ 输入（明文或密钥）即使只有很小的变化，也会导致输出发生巨大变化的现象

✓ 明文的一个比特的变化应该引起密文许多比特（从安全的角度一般要求接近密文长度的一半）的改变

雪崩效应：这与P盒的功能有关，是混淆-扩散特性的进一步反映，要求有良好的雪崩效果，即要求当输入有一比特发生变化时，将导致输出有一半的比特位发生变化

轮函数F的设计准则

轮函数F通常是指迭代分组密码中单轮加密算法的非线性函数，其设计准则就是保证非线性度要强，具体通过位独立和雪崩效应来实现更加混乱

指标：

  • 安全性：轮函数F必须能抵抗所有已知的密码攻击方法，尤其是抵抗差分密码分析和线性密码分析
  • 速度：what can i say，nothing
  • 灵活性：支持密码算法能在多平台和多处理器上实现

Feistel密码结构的核心，实现依赖于S盒。设计准则包括非线性、雪崩效应准则和位独立准则。

位独立准则要求输入中某一位的变化，引起输出中其他位的变化应是彼此无关的

迭代轮数的考虑

  • 一般来说，分组密码迭代轮数越多，密码分析越困难
  • 但也不是追求迭代轮数越多越好，多会使结构复杂化，分组密码迭代轮数一般采用\(r = 8,10,12,16,20\)的居多
  • 设计迭代轮数的准则是：使密码分析的难度大于简单穷举攻击的难度

密钥扩展算法的设计

密钥扩展是迭代分组密码算法的一个重要组成部分，是从初始（种子）密钥产生迭代各轮要使用的子密钥的算法

评价指标：

  • 结构尽量简单，便于软硬件实现
  • 密钥扩展算法至少应保证密钥和密文符合位独立准则和严格雪崩效应准则
  • 不存在简单数学关系，获取前后的位比特联系在计算上是困难的
  • 没有弱密钥，弱密钥通常是指因设计不当或不可避免存在的会明显降低密码算法安全性的一类密钥
  • 保证种子密钥的各比特对每个子密钥比特影响的均衡性
  • 速度也是衡量子密钥扩展的一个重要指标

子密钥的生成方法： 理论设计目标是子密钥的统计独立性和密钥更换的有效性

对称密码

对称密钥算法(Symmetric-key algorithm)，又称为对称加密、私钥加密、共享密钥加密，是密码学中的一类加密算法。

对称加密的特点是，在加密和解密时使用相同的密钥，或是使用两个可以简单地相互推算的密钥。

对称加密的优点是速度快，缺点是需要共享密钥，安全性不足。

​ 在没有非对称密码之前，我们所有的密码方案都属于对称密码，如今我们一般特指对称密码中的块密码指代对称密码，我们在RSA中了解了对称密码的缺点，并且了解了非对称密码的优点，那么为什么还需要使用对称密码呢？实际上对称密码还拥有非对称密码不可比拟的一个优点则是：快。

​ 实际上，可能会考虑非对称密码密钥过长，算法较复杂，需要分块设计填充算法等等，这些都不是最重要的缺点，最主要的便是非对称密码和对称密码比起来在同等性能下实在是太慢了。甚至部分小功耗设备性能不足以支持运行一些非对称密码。所以对称密码依然广泛运用于我们的现实生活中，大部分的对称加密算法都是基于ARX操作，即加法Add，移位Rotate，异或Xor，在速度上相对于非对称密码复杂的幂、指数和函数运算来说天生有着绝对的优势。

对称加密算法可分为两大类型:

  • 分组加密： 先将明文切分成一个个固定大小的块，再对每个块进行加密，这种方式被称为分组加密或块加密，有的资料称呼为"分组密码"或"块密码"。
  • 流加密：将密钥扩展到与密文等长后，用扩展后的密钥与明文按比特位做异或运算

相比分组加密，流加密具有速度快，消耗少的优点，在网络通信的某些特定场景比较有优势。然而流加密的发展落后于分组加密，其安全性、可扩展性、使用灵活性上，目前认为还是比不上分组加密的，同时某些分组加密算法可以兼具流加密的部分特点。因此对称加密的主流仍然是分组加密。

常见的流加密算法如RC4、ChaCha20等等，它们的安全强度主要取决于扩展后密钥的随机性。

流加密不是本章的学习重点，这里只简单了解一下，接下来开始学习分组加密，后文提到对称加密时，一般都是特指分组加密。

分组密码的操作模式

电子密码本模式（ECB）

 Electronic Codebook Mode，简称为ECB模式

 明文被每次处理64位，若最后一块不足64位，则用一些任意二进制序列填充

 每个明文分组都用同一个密钥加密，这样相同的明文块总被加密成相同的密文块

 算法逻辑： \[ (\text{加密)}C_j=E_k(P_j)(j=1,2,...,N)\\(\text{解密)}P_j=D_k(C_j)(j=1,2,...,N) \]

ECB

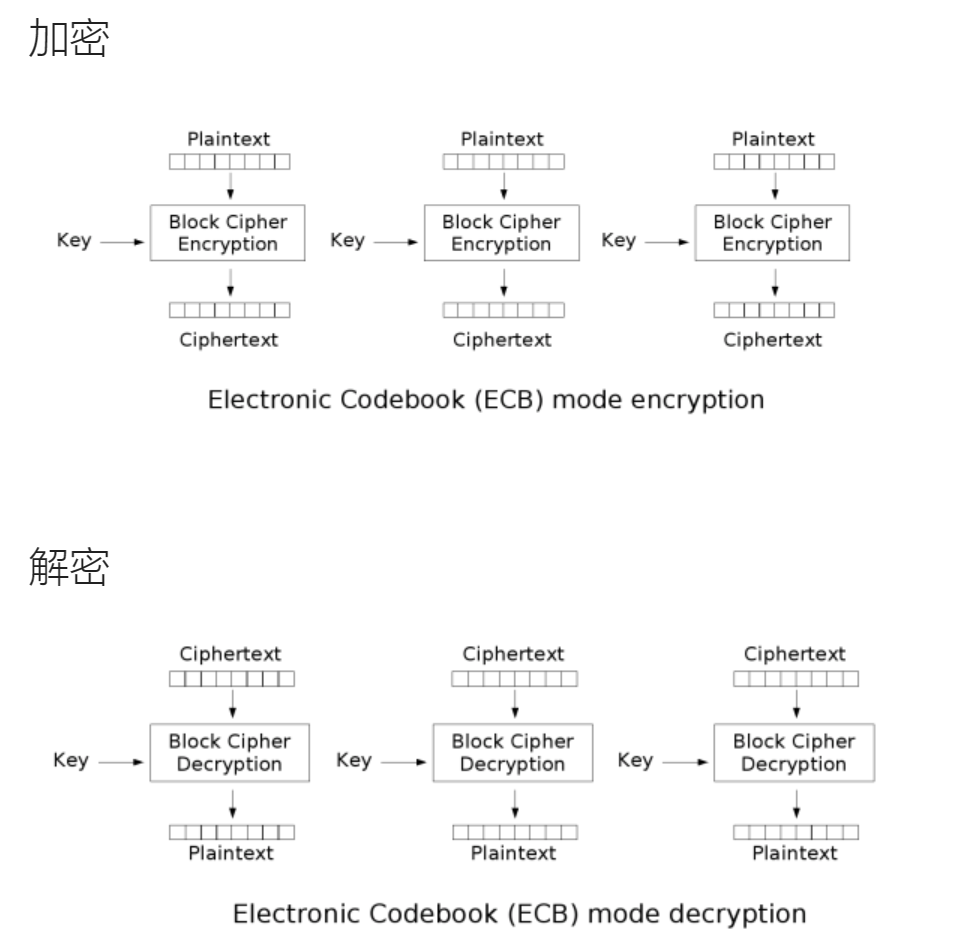
特点：

  • 操作模式简单，不同的分组可以并行处理
  • 明文中的重复内容将在密文中表现出来，特别对于图像数据和明文变化较少的数据
  • 不具有错误传播特性，即如果一个分组中出现传输错误不会影响其他分组
  • 主要用于内容较短（不超过一个分组）的报文的加密传递

密码分组链接模式(CBC)

Cipher Block Chaining Mode，简称为CBC模式

加密函数的输入是当前的明文分组和前一个密文分组的异或

算法逻辑： \[ (\text{加密)}C_1=E_k(P_1\oplus\mathrm{IV})，C_j=E_k(P_j\oplus C_{j-1})(j=2,...,N)\\ (\text{解密)}P_1=D_k(C_1)\oplus\mathrm{IV}，P_j=D_k(C_j)\oplus C_{j-1}(j=2,...,N)\\ （IV称为初始向量） \]

CBC

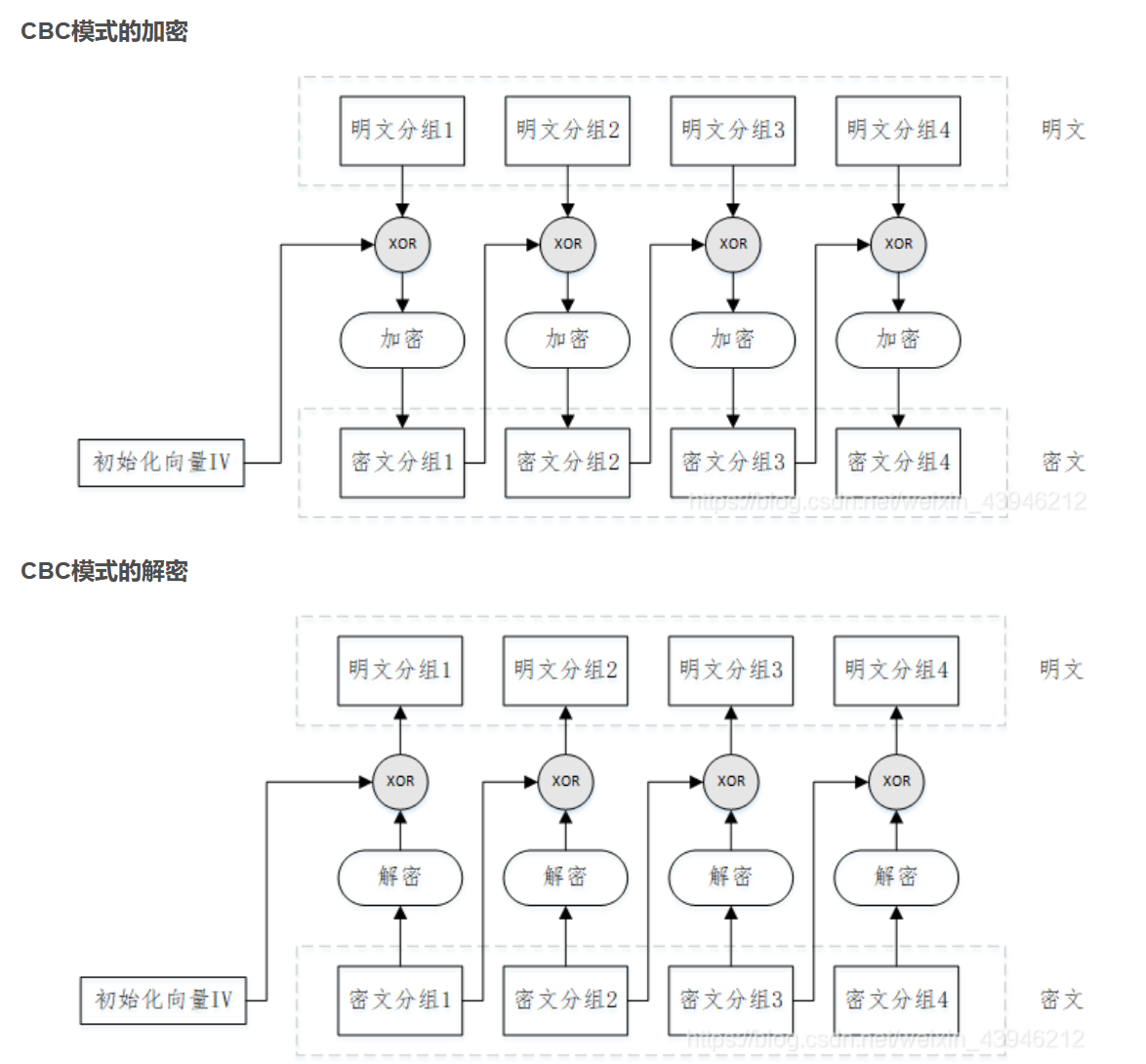
特点

  • 同一个消息中的两个相同的明文被加密成不同的密文
  • 若不同消息的前若干个分组相同，且加密时使用相同的IV，这些分组的加密结果将一致。此时以时间戳作为IV较好
  • 密文分组中的一位出错具有自恢复能力，即若密文块\(C_j\)在传送过程中出错，则解密时会造成\(P_j\)和\(P_{j+1}\)两个明文块都出错，但后面的密文块仍然能自动正确恢复
  • 可用于加密和认证。用于加密时不能并行处理，也不能用于加密或解密可随机访问的文件记录（因为该模式需要访问以前的记录）

计数器模式（CTR）

Counter Mode，简称为CTR模式

使用与明文分组规模相同的计数器长度，但要求加密不同的分组所用的计数器值必须不同

计数器值经加密函数变换的结果再与明文分组异或，从而得到密文

解密使用相同的计数器值序列，用加密函数变换后的计数器值与密文分组异或，从而恢复明文

算法逻辑： \[ (\text{加密)}C_j=P_j\oplus E_k(\text{CTR}+j)(j=1,2,...,N)\\(\text{解密)}P_j=C_j\oplus E_k(\text{CTR}+j)(j=1,2,...,N) \]

CTR

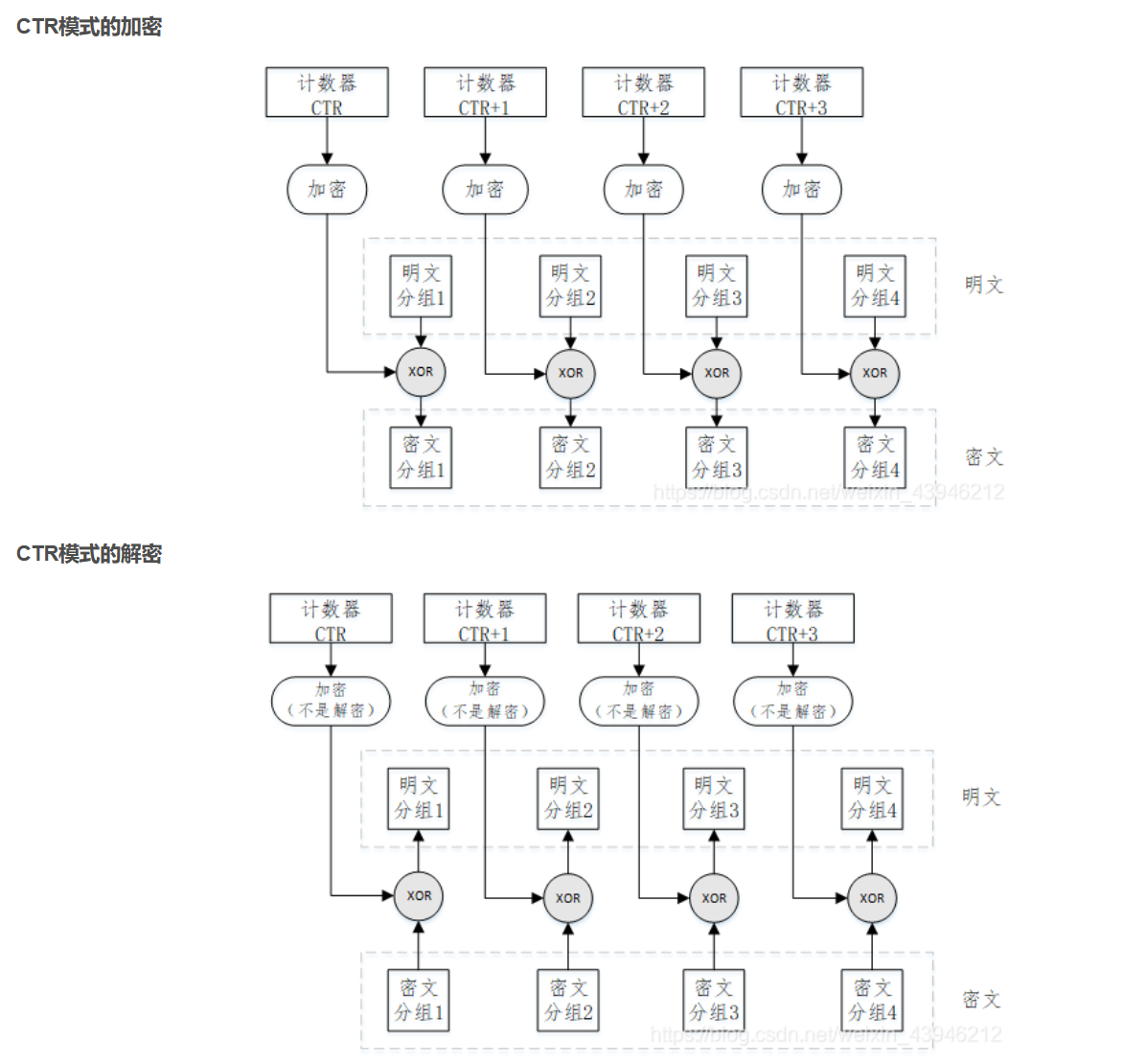
特点

  • 处理效率高，可进行并行处理，提高数据吞吐量
  • 可提前进行预处理
  • 具有随机访问特性，可随机对任意一个密文分组进行解密处理，对该密文分组的处理与其他密文无关
  • 实现简单，加、解密阶段都只涉及加密函数。（这点与ECB和CBC模式不同）
  • 适于对实时性和速度要求较高的场合

密码反馈模式(CFB)

Cipher FeedBack Mode，简称为CFB模式

  • 加密算法的输入是64比特移位寄存器，其初值为某个初始向量IV
  • 加密算法输出的最左（最高有效位）\(j\) 比特与明文的第一个单元\(P_1\)异或，产生出密文的第一个单元\(C_1\)
  • 将移位寄存器的内容左移\(j\)位并将\(C_1\)送入移位寄存器最右边（最低有效位）\(j\)位
  • 解密时，将收到的密文单元与加密函数的输出进行异或\((仍然使用加密算法)\)

算法逻辑： \[ \begin{aligned}&\text{(加密)}C_1=P_1\oplus S_j[E_k(\mathrm{IV})]，C_i=P_i\oplus S_j[E_k(\mathrm{SR}_j||C_{i-1})](i=2,...,N)\\ &(\text{解密)}P_1=C_1\oplus S_j[E_k(\mathrm{IV})]，P_i=C_i\oplus S_j[E_k(\mathrm{SR}_j||C_{i-1})](i=2,...,N)\\ &\text{式中,}S_j[x]\text{表示}x\text{的最左边}j\text{位,SR}_j\text{表示移位寄存器SR左移}j{位,}\|\text{表示连接关系}\end{aligned} \]

输出反馈模式(OFB)

DES

下面主要是Xenny师傅的内容，而不是赖师父的内容了

  • DES是一种典型的块加密，即将明文分成一块一块的数据，分别进行加密再进行拼接得到密文。

    在DES中，具有如下特点

    1. 输入64位。

    2. 输出64位。

    3. 密钥64位，使用64位密钥中的56位，剩余的8位要么丢弃，要么作为奇偶校验位。

    4. 采用Feistel迭代结构：

      1. 明文经过 16 轮迭代得到密文。
      2. 密文经过类似的 16 轮迭代得到明文。

  • 其实Feistel是用来构建块加密算法的对称结构，但是从CTF的实际角度来说，我们并不从Feistel开始介绍而是直接介绍DES，有关Feistel迭代结构的详细介绍可以参考

    https://zhuanlan.zhihu.com/p/381026295

    在这里我们只需要了解Feistel是一种轮次迭代方式即可。

DES密码算法采用Feistel密码的S-P结构，其特点是：加密和解密使用同一算法、同一密钥、同一结构

区别是：16轮加密子密钥顺序为\(K_1,K_2,\cdots,K_{16}\)，解密子密钥顺序为\(K_{16},K_{15},\cdots K_{1}\)

三个阶段：初始置换、乘积变换和逆初始置换

待补充

IDEA

AES

参考：

现代密码学常用符号总结 - Max1z - 博客园 (cnblogs.com)

密码学之安全模型总结 - Max1z - 博客园 (cnblogs.com)

Diffie-Hellman 密钥交换和 Elgamal 加密算法 (ruanx.net)

一文搞懂Diffie-Hellman密钥交换协议 - 知乎 (zhihu.com)

(´∇｀) 被你发现啦~ ELGamal加密方案不是CCA安全 | Hexo (gejiangxia.github.io)

《现代密码学》 - WittPeng - 博客园 (cnblogs.com)

#密码学
密码学-3-分组密码
http://viper2383.github.io/2024/04/21/密码学导论-3-分组密码/
作者
w1per3
发布于
2024年4月21日
许可协议