密码学-4
本文最后更新于:2024年5月16日 早上
公钥密码学
公钥密码体制的模型
- 公钥密码体制在加密和解密时使用不同的密钥,这样通信双方无须预先交换密钥就可以建立保密通信。克服了对称密码体制中通信双方必须使用一个安全信道预先约定密钥的缺点
- 在公钥密码体制中,每个用户保存一对密钥,即公钥PK和私钥SK,PK是公开信息,不需要保密。虽然公钥密码体制的私钥SK和公钥PK是成对出现的,但给定公钥,要确定出私钥是计算上不可行的。持有公钥的任何人都可以加密明文产生密文,只有持有私钥的人才能够解密
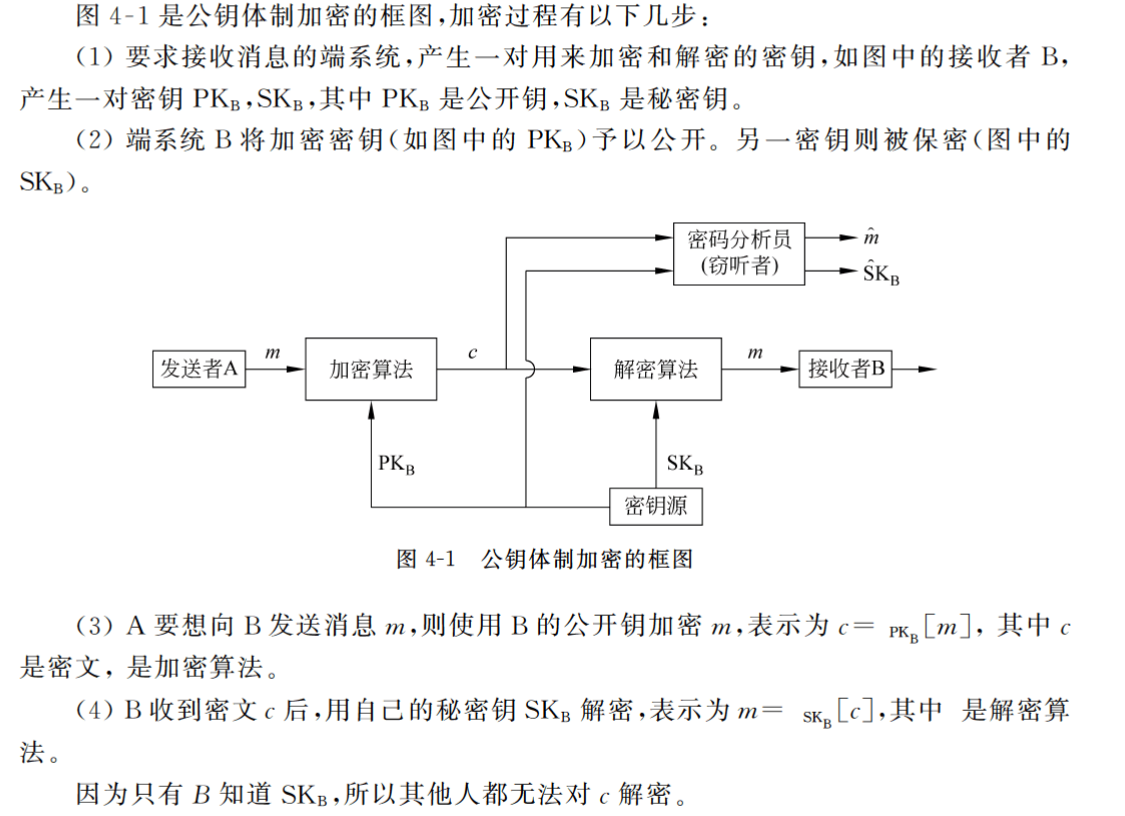
公钥密码体制的基本原理
用抽象的观点来看,公钥密码体制就是一种陷门单向函数
单向函数是满足下列条件的函数:
它是定义域到值域的一个映射,同时还要满足下列条件: 计算函数值是容易的,而从函数值计算原像是不可行的.
陷门单向函数是这样的单向函数,存在一个附加信息,当不知道该附加信息时,从函数值求原像是困难的,但当知道该附加信息时,从函数值求原像就变得容易了。
即陷门单向函数在附加信息未知时是单向函数,而当附加信息已知时,就不再是单向函数了。通常把附加信息称为陷门信息。

公钥密码体制就是基于这一原理而设计的,利用一个陷门单向函数,将它作为公开密钥,而将陷门信息作为秘密密钥.。其安全强度取决于它所依据的问题的计算复杂度
公钥密码体制的要求
- 产生一对密钥在计算上是可行的
- 已知公钥和明文,产生密文是容易的
- 接收方利用私钥来解密密文在计算上是可行的
- 对于攻击者,利用公钥来推断私钥在计算上是不可行的
- 已知公钥和密文,在不知道私钥的情况下,恢复明文在计算上是不可行的
RSA公钥密码体制
RSA公钥密码体制是美国麻省理工学院的Rivest,Shamir和Adleman三位学者于1978年提出的。RSA公钥密体制的理论基础是数论中的大整数因子分解的困难性。RSA公钥密码体制即可用于加密,又可用于数字签名。它安全、易懂、易实现,是目前广泛应用的一种密码体制。
事实上,Cliff Cocks 在1973年发表的题为“关于非对称加密的注记”文章中,就描述了跟RSA密码体制基本一致的方案
密钥生成算法\(KeyGen\):
- 选两个大质数p和q,且 \(p!=q\),计算 \(N=p*q\),N就算出来了
- 然后计算N的欧拉函数 \(φ(N)=(p-1)(q-1)\)
- 然后你自己选个e, \(1<e<φ(N)\),且与φ(N)互质,
- 为什么e与φ(N)互素:要存在d,互素才存在这样一个d
- 由e和φ(N)互质,\((e,φ(N))=1\),再由辗转相除法,则一定有\(ed - φ(N)k = 1\)
- 那么由e就可以算出d,\(ed ≡ 1\quad
mod(φ(N))\)
- pk(公钥):N,e
- sk(私钥):d
p,q是秘密参数,需要保密,如不需要保存,可销毁
加解密:
\[ \begin{align} Enc(pk,m∈Z_N^*):c = m^e\ mod \ N\\ Dec(sk,c): m = c^d\ mod\ N \end{align} \]
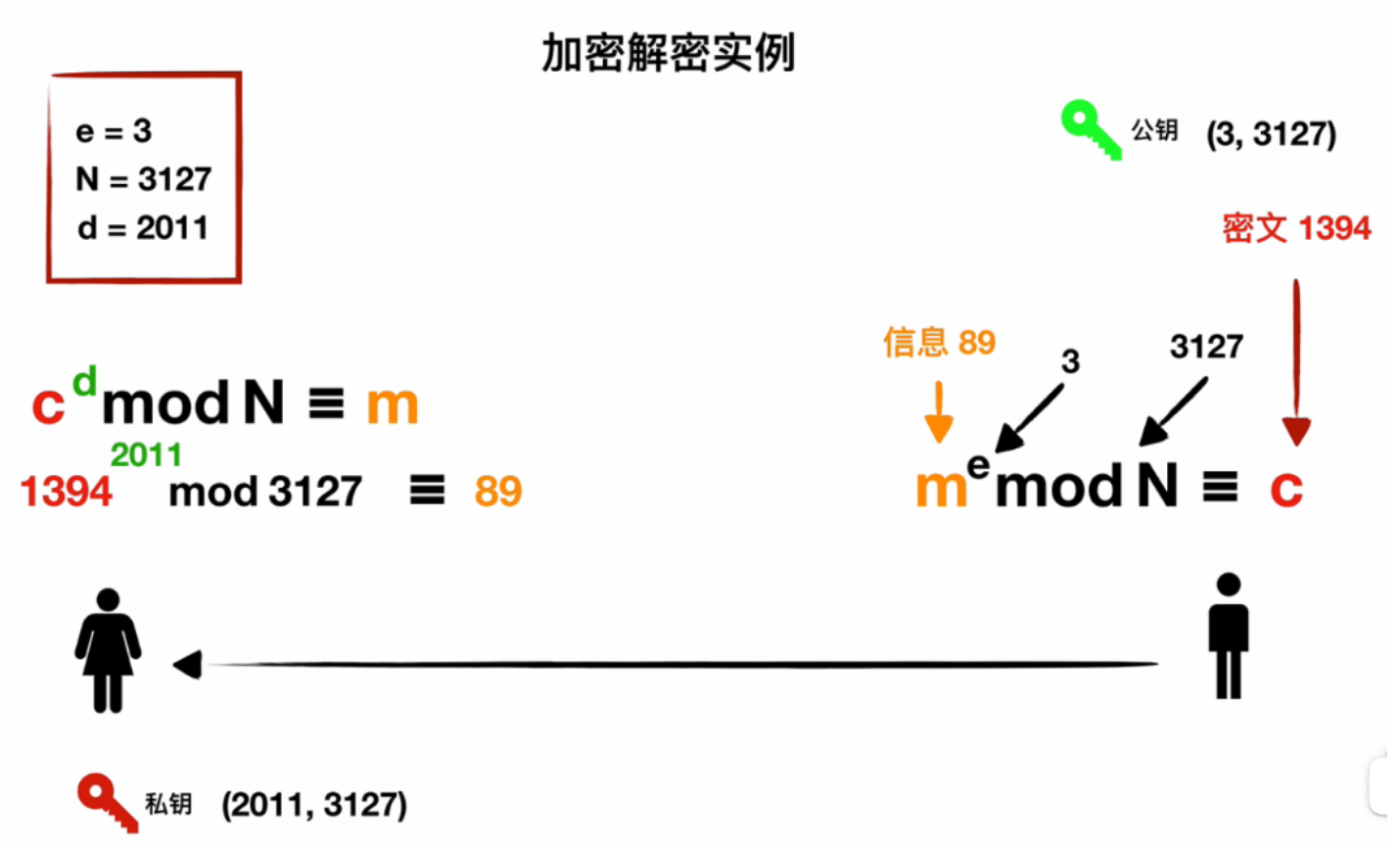
正确性证明
\[ \begin{align} &即验证 c^d modN 是否等于 m\\ &∵ed ≡ 1\quad mod(φ(N))\\ &∴ed = kφ(N) + 1\\ &即验证m^{ed} mod N最后是等于m的\\ &m^{kφ(N) + 1} \quad mod \quad N \\ &m^{kφ(N)}*m \quad mod \quad N\\ &即求:m^{φ(N)}≡1modN\\ &∵m∈Z_N^*\\ &g^{ord(G)} = 1(单位元)\\ &∴m^{φ(N)}≡1modN &\end{align} \]
对于
\[ \begin{align} &m∈Z_N(放大m的范围了)\\ &m \notin Z_N^*\\ &∵ N =p*q\\ &∴gcd(m,N)=p或q\\ &这里的情况N直接分解出来了\\ &若gcd(m,N)=p,m<N,N=p*q\\ &得m=kp,1≤k<q\\ &gcd(m,q)= 1\\ &相当于m∈Z_q^*,则m^{φ(q)}=1modq\\ &m^{q-1}=1modq\\ &ed = k^{'}φ(N)+1=k^{'}(p-1)(q-1)+1\\ &m^{k^{'}(p-1)(q-1)} =1modq\\ &m^{k^{'}φ(N)} =1modq\\ &即m^{k^{'}φ(N)} =rq+1\\ &我们这里还是要求m^{ed}modN最后等于m\\ &m^{k^{'}φ(N)}*m \quad mod N\\ &=(rq+1)m \quad modN\\ &=(rqm+m)\quad mod N\\ &=(rq*kp+m)\quad mod N\\ &=(rkN+m)\quad mod N\\ &=m \end{align} \]
RSA问题,给定N,e,\(y∈Z_N^*\),求x,满足\(x^e=y\ mod\ N\)
一个密文对应一个明文,所以jzlaoshi不把RSA叫做一个加密方案,而是一个单向陷门置换
RSA公钥密码体制的安全性
RSA是建立在大整数分解的困难性之上的
大整数分解攻击:一旦分解出p和q,就可以得到n的欧拉数φ(N),再利用欧几里德扩展算法求出RSA 的私钥d.
因此,应当采用足够大的大整数n(至少应取1024位,最好为2048位)。此外,对素数p和q的选取应满足以下要求:
- p和q的长度应该相差不大
- (p - 1)和(q - 1)都应该包含大的素因子
- gcd(p - 1,q -1)应该尽可能小
- d < n,且\(d<n^{0.294}\),特别是当\(d<n^{1/4}\)时,已经有办法攻破RSA
ElGamal公钥密码体制
ElGamal加密算法是一个基于Diffie-Hellman密钥交换的非对称加密算法,
离散对数问题: \[ G,p,g,,,h∈G,求x∈Z_p,使得h = g^x \]

加密算法的第一行写错了,应该为m ∈ G
公钥密码体制的安全模型

OW-CCA 比 OW-CPA安全性高
IND-CCA 比 IND-CPA安全性高
IND-CCA 比 OW-CCA高
也就是说 CCA安全一定是CPA安全,但CPA安全不一定是CCA安全,
IND-CPA
示意图:
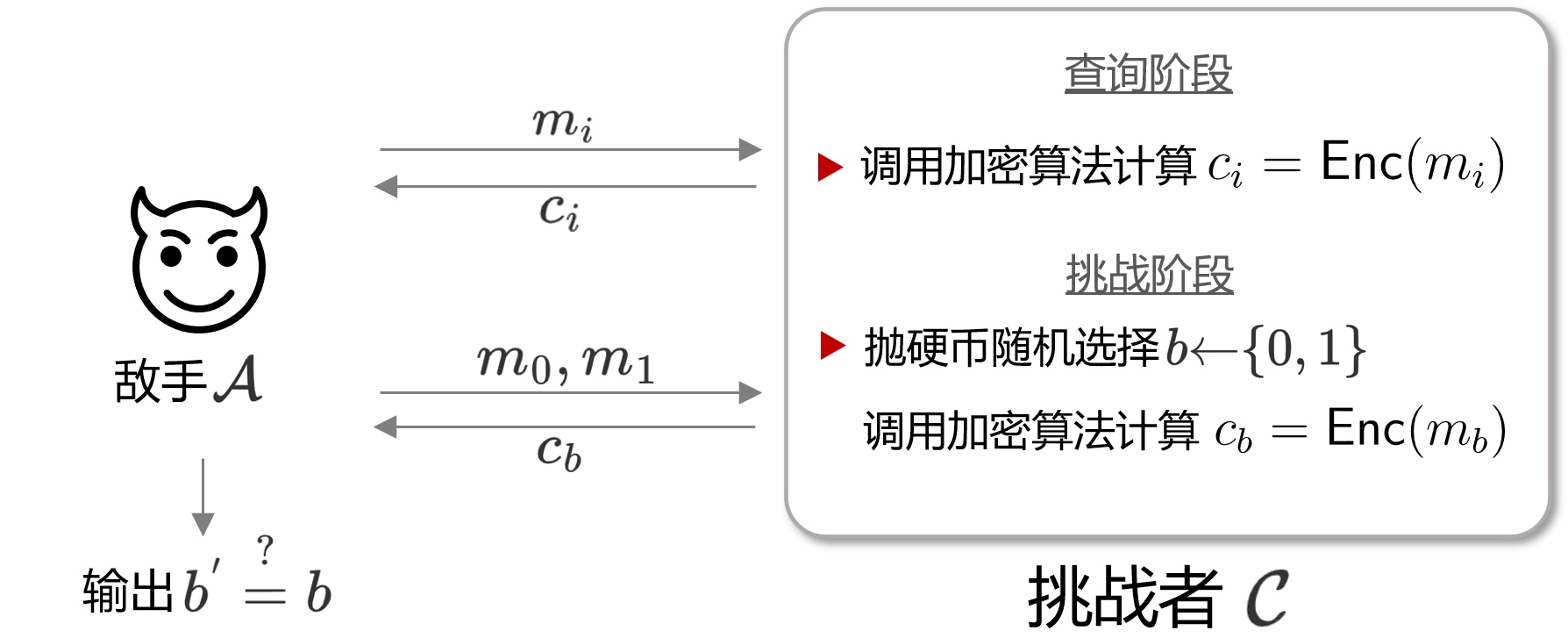
IND-CPA所表示的含义为,在敌手能自行选择明文,并查询对应密文这一模型中,我们的加密算法是否还能实现密文不可区分。在这一Game中,敌手可以查询任意一条明文消息对应的密文, 这需要我们开放自己算法的加密功能给敌手
IND-CPA这一Game的步骤如下:

这里的Pr是计算某一事件的概率
可以看出,IND-CPA实际上是想表达“如果密文足够随机的话,密文是不会泄露任何关于明文信息”这一深层含义
任意一个公钥加密方案,如果加密算法是一个确定的算法,它永远不可能达到IND-CPA安全。如:RSA就达不到,一个明文对应一个密文
IND-CCA
ElGamal不是IND-CCA安全
IND-CCA2

数字签名
概述
在传统商务活动中,为了保证交易的安全与真实,一份书面合同或公文要由当事人或其负责人签字、盖章,以便让交易双方识别是谁签的合同,保证签字或盖章的人认可合同的内容,在法律上才能承认这份合同是有效的。
而在电子商务的虚拟世界中,合同或文件是以电子文件的形式表现和传递的。在电子文件上,传统的手写签名和盖章是无法进行的,这就必须依靠技术手段来替代。
数字签名就是能起到手写签名或者盖章同等作用的电子技术手段。
数字签名已成为计算机网络不可缺少的一项安全技术措施是实现认证的重要工具。数字签名在商业、金融、军事等领域,特别是在电子贸易、电子支票、电子购物、电子政务及知识产权保护等方面的应用,有力地显示了数字签名的重要性。
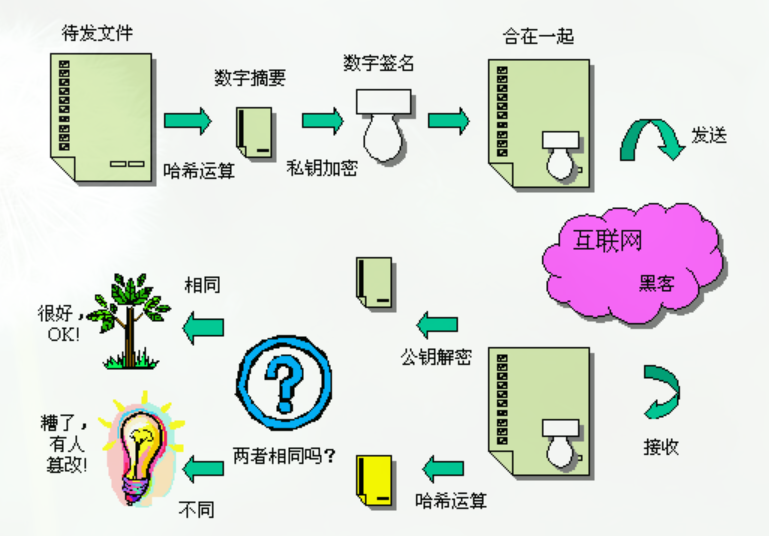
数字签名的特征
- 收方能够确认或证实发方的签名,但不能伪造
- 发方发出签名的消息给收方后,就不能再否认他所签发的消息。
- 收方对已收到的签名消息不能否认。
- 第三者可以确认收发双方之间的消息传送,但不能伪造这一过程。

Hash函数
先简单了解一下
Hash函数的基本需求:
在深入Hash函数的安全性之前,我们首先需要了解它们必须满足的基本需求:
- 确定性:对于任何给定的输入,Hash函数总是返回相同的输出。这意味着无论你何时何地运行Hash函数,对同一数据的Hash值总是不变的。
- 快速计算:无论数据大小如何,Hash函数都能迅速计算出Hash值。这对于处理大量数据或需要实时处理的系统尤为重要。
- 抗碰撞性:即使是微小的输入变化,也会导致输出(Hash值)的巨大变化。这使得预测或生成具有相同Hash值的两个不同输入非常困难。
Hash函数的安全性挑战:
尽管Hash函数的设计旨在满足上述需求,但在现实世界的应用中,它们面临着许多安全挑战:
抗碰撞攻击:理想的Hash函数应该抵抗碰撞攻击,即很难找到两个不同的输入但产生相同的Hash值。然而,随着计算能力的增强和算法的发展,某些Hash函数已经被证明容易受到碰撞攻击。
预映像和二次预映像攻击:这些攻击尝试找到一个输入,使其Hash值等于特定的Hash值(预映像)或找到一个不同的输入,使其Hash值与另一给定输入的Hash值相同(二次预映像)。强大的Hash函数应该能有效抵抗这类攻击。
速度与安全性的折中:在某些应用中,如密码学货币,Hash函数需要足够的“慢”以抵抗暴力攻击,而在其他应用中,如网络数据处理,需要足够快的Hash算法以维持效率。找到这种平衡是设计Hash函数时的一个挑战。、
实践中的Hash函数:
在实践中,已经开发了多种Hash函数来满足不同的需求和抵抗各种攻击。例如:
- MD5:一度广泛使用,但现在已被证实容易受到碰撞攻击,因此不再推荐用于安全敏感的应用。
- SHA系列:包括SHA-1、SHA-256等,是目前广泛认可和使用的Hash算法。尽管某些较早的版本如SHA-1也显示出安全弱点,但更新版本如SHA-256仍被认为是安全的。
- bcrypt和Argon2:这些是专为密码存储设计的Hash函数,通过增加计算成本来抵抗暴力攻击。
RSA签名方案
\[ \begin{align} &m_1*σ_1 = m_1^d \mod N\\ &m_2*σ_2 = m_2^d \mod N\\ &m =m_1*m_2,σ =σ_1*σ_2\\ &两个相乘 m*σ = (m_1m_2)^d \mod N\\ &也就是说我知道两个就能构造第三个,(其实知道一个就可以了\\ &所以是不安全的\\ &可以利用一个安全的Hash函数 H 来产生消息摘要H(m);\\ &H(m_1,m_2)≠H(m_1)*H(m_2)\\ \end{align} \]
所以直接拿来做签名是不安全
要改一改:利用一个安全的Hash函数 H 来产生消息摘要H(m),哈希函数是一个单向函数

安全性:
- 签名时使用了Hash函数可以防止利用同态的伪造攻击,有很好的抗攻击性。
- RSA签名方案存在签名可重用的问题,同一消息在不同时刻签名不应是相同的。
ElGamal签名方案

签名算法中:
g是\(Z_p^*\)的生成元,但是实际上中很难取到,所以一般设置\(p-1=rq\),所以\(Z_p^*\)中存在一个q阶的子群,随便在\(Z_p^*\)中选一个h,作\(h^r\),则\(g=h^r\)一定是生成元 (对吗?😥😥
\(gcd(k,p-1)\),才能保证\(k \mod p-1\)有逆元,才能算出来s
定义:生成元的阶就是群的阶,这里就是\(p-1\),所以\(0<k<p-1\),k只能在这个范围,\(p-1\)就是最大的了
这里的群的阶最大就是\(p-1\)
Schnorr签名方案

签名验证算法中可以给\(σ=(e,s)\),也可以给\((R,s)\),大部分都选前者
原因:计算开销是一样的,不管给谁R,e,s都是要算的,所以看通信的消耗size,R是群中的元素,表示群元素至少要\(log_2p\)位,e是mod之后的,所以e的位数要小一点
公布\((e,s)\)作为签名:
计算\(R'=g^s*y^e\)
验证 \(e\ 等于or不等于\ H(m,R')\)
这里假设 \(s=r-ex\) 是对滴,那么\(g^s=g^{r-ex}=g^r*(g^x)^{-e}=g^r*y^{-e}=R*y^{-e}\)
公布\((R,s)\)作为签名:
计算\(e=H(m,R)\)
验证 \(g^s =or≠ R*y^{-e}\)
\(g^s=g^{r-ex}=g^r*(g^x)^{-e}=g^r*y^{-e}=R*y^{-e}\)
数字签名标准
更习惯于叫它DSA

DSA这里\(g\)的阶是\(q\),因为\(q\)是素数,所以k的逆元一定存在,所以这里的k<p就行了,跟上面比少了一个\(gcd(k,p-1)\)的条件
ElGamal签名方案g的阶是p-1
跟ElGamal签名方案的构造本质上是一样的,不过不再作用在\(Z_p^*\),而是它的一个子群中
\[ ElGamal签名方案:r=g^k\ mod\ p,s=k^{-1}(H(m)-xr)\ mod\ p-1,0<k<p-1\\ 数字签名标准(DSA):r=(g^k\ mod\ p )\ mod\ q,s=k^{-1}(H(m)+xr)\ mod\ q,0<k<q \] \(Z_p^* ,*\mod p,ElGamal签名方案种,g是这个群的生成元\)
DSS算法的详细解释(简单易懂版)
(1)DSS算法的主要参数:
全局公开密钥分量:
- 素数p, \(2 ^ {511} < p < 2 ^ {512}\);
- q是(p-1)的一个素因子, \(2^{159} < q < 2^{160}\);
- \(g=h ^ {[(p-1)/q]} mod p\), 其中h是一整数,\(1<h<(p-1)\)
私钥:
私钥x是随机或伪随机整数, 其中\(0<x<q\);
公钥:
\(y=g ^ x mod p\),\((p,q,g,y)\)为公钥;
用户的随机选择数:
k为随机或伪随机整数, 其中\(0<k<q\)
(2)DSS的签名过程:
\(r=(g ^ k \mod p) \mod q\),这里又mod q,再做了一次压缩,这是跟ElGamal最大的差别
\(s=[k ^ {-1} (H(M)-xr)] \mod q\)
形成了对信息M的数字签名(r,s),数字签名和信息M一同发送给接收方。接收方接收到信息M’和数字签名(r’,s’)后,对数字签名的验证过程如下:
\(w=(s’) ^ {-1} \mod q\)
\(u1=[H(M’)w] \mod q,\)
\(u2=( r’) w \mod q\)
\(v=[(g ^ {u1} y ^ {u2}) \mod p] \mod q\)
如果 \(v= r’\),则说明信息确实来自发送方。
lai:
\(k=s^{-1}(H(m)+xr)\mod q\)
g的阶是q
\(g^k=g^{s^{-1}(H(m)+xr)}=g^{s^{-1}H(m)+s^{-1}xr}=g^{s^{-1}H(m)}*y^{s^{-1}r} \mod p \mod q\)
看\(g^{s^{-1}H(m)}*y^{s^{-1}r} \mod p \mod q\)是否等于r
DSS签名的正确性
因为 \((u_{1}+ xu_{2}) \mod q= ( H( m) + xr) s^{- 1} \mod q= k\)
所以:
\[ \begin{align} &g^{u_1}y^{u_2} \mod\ p \mod\ q\\ &= g^{u_1}g^{xu_2} \mod p \mod q\\ &= g^{u_1+ xu_2} \mod p \mod q\\ &= g^{k} \mod p \mod q,这一步是为什么呢?\\ &=r\\ \end{align} \]
上面的问题,我是这样想的:
其实就是同余的基本性质
若\((u_{1}+ xu_{2}) \mod q= k\)
则\(g^{u_1+ xu_2} \mod p \mod q= g^{k} \mod p \mod q\)
从群的角度来看,其实ElGamal和DSA是一样的,但是在计算r的时候又mod q,如果不mod q的话,其实两个方案就是一样的
签名的安全模型
EUF-CMA
或EU-CMA,选择消息攻击下的存在性不可伪造:Existential Unforgeability under Chosen Messagge Attack
这一模型中的CMA指Chosen Message Attack,即选择消息攻击,本质上与CPA其实是一样的,只不过在数字签名等算法中,用消息一词要比明文更加贴切。CMA和CPA都是形容敌手能自由地向算法提交输入并获得的相应输出这一能力。
意思就是:你可以要任何消息的签名,但是你不能造出一个一样的签名
EUF则是指存在性不可伪造,即 Existential UnForgeability,指的是对于消息认证、数字签名等算法而言,当敌手通过查询获得了 q 个签名后, 他无法再获得第 q+1个签名。这一Game的示意图如下所示:
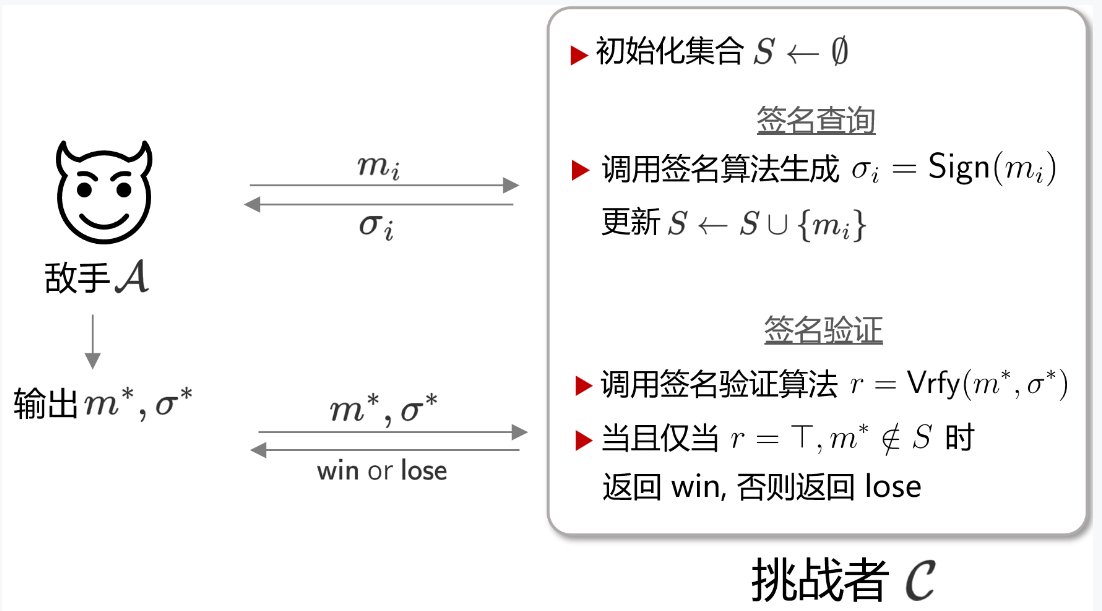
可以看到,其基本形式依然和前文的模型保持相似,在查询阶段,敌手 \(\mathcal{A}\) 可不断与一实现了签名Oracle的 \(\mathcal{C}\) 交互,来获得所提交消息 \(m\) 的签名 \(\sigma\) 。在进行 \(q\) 次交互后,敌手将输出一对 \(\left(m^*, \sigma^*\right)\) 。这一Game的主要步骤为:
- Game中拥有一具有多项式资源的敌手 \(\mathcal{A}\) 和一个能自由调用签名算法oracle \(E\) 的挑战者 \(\mathcal{C}\) 。
- \(\mathcal{C}\) 随机选取 \(sk\stackrel{\$}{\leftarrow}\{0,1\}^n\) ,作为签名算法的私钥
- \(\mathcal{A}\) 向 \(\mathcal{C}\) 提交消息 \(m, \mathcal{C}\) 得到 \(m\) 对应的签名 \(\sigma\)
- 重复步骤 \(3 q\) 次 (即敌手查询 \(q\) 次不同消息的签名)
- \(\mathcal{A}\) 输出一对 \(\left(m^*, \sigma^*\right)\);
- \(\mathcal{C}\) 对 \(\sigma^*\) 进行验证,并返回验证结果;
若最后敌手输出的 \(m^*\) 未曾被查询过,且 \(\sigma^*\) 能通过验证,就可认为敌手挑战成功。这一结果即为 “签名的伪造”,此处敌手的优势可写为: \[ \operatorname{Adv}_S^{\text {EUF-CMA }}(\mathcal{A})=\operatorname{Pr}\left[\mathcal{A} \text { forges }\left(m^*, \sigma^*\right)\right] \]

SUF-CMA
或SU-CMA,选择消息攻击下的强不可伪造性:Strong Unforgeability under Chosen Messagge Attack
在EUF-CMA中,E表示的是Existential,而此处的SUF的S则表示Strong,即强不可伪造性,这一Game的基本模型如下图所示。
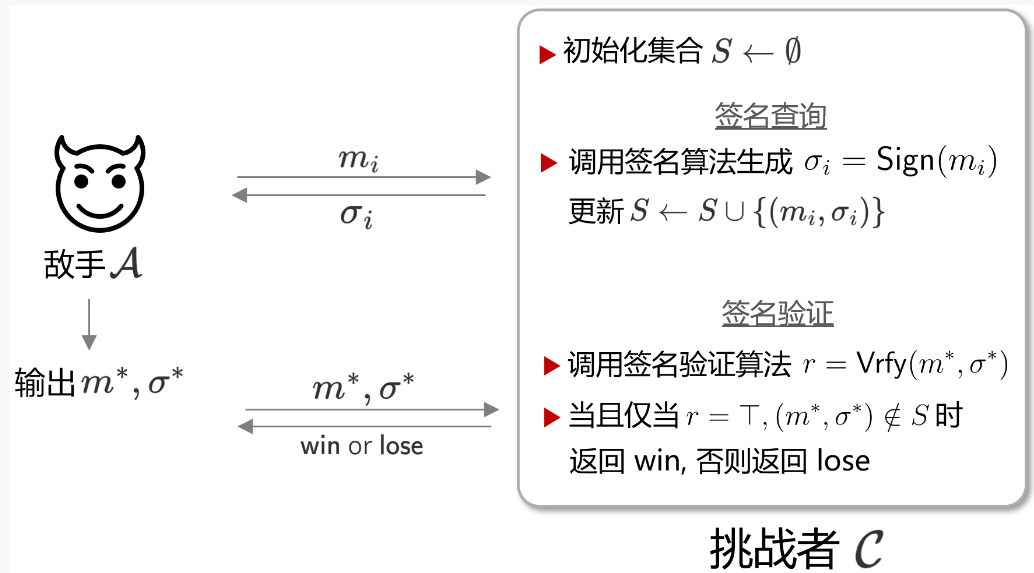
与EUF-CMA相比,SUF-CMA唯一的不同之处在于敌手最终输出伪造的签名对 \((m^∗,σ^∗)\)时,不仅要求 \(m^∗\)是未曾查询过的,也要求签名\(σ^∗\)是未曾出现过的。
因此,EUF-CMA这一Game中的敌手只需要寻找到 m 关于 σ 的一个碰撞即可,而在SUF-CMA中,敌手的任务并不是要找碰撞,而是要从根本上伪造出一个签名消息对。
总结一下:
这里的签名的安全模型规定的这些东西,对数字签名本身的功能来讲,功能不大,因为相当于你伪造了一个我的章发出去,可是我已经用我的章发出去了, 你伪造一个跟我一样的章发出去,对我没影响,我消息发出去了(只是当成一个签名)
但是用数字签名方案构造其他东西的时候,会有用,也就是说可以把数字签名方案当成一个部件,去搭建更🐂🖊的功能
- 一个证明题
以下两种证明的表述是一样的:
证明:如果一个数字签名方案,它的签名算法是一个确定性的算法,那么这个方案对EUF-CMA和SUF-CMA的安全性是一样的
证明:如果一个数字签名方案,它的签名算法是一个确定性的算法,它是EUF-CMA安全的,那么这个方案也是SUF-CMA的
我们讲的签名方案中,只有RSA是确定性的算法
因为\(SUF-CMA⟹EUF-CMA\)是肯定成立的
上面的证明就是要证明:
如果一个签名方案其签名算法是确定性的算法,那么\(EUF-CMA⟹SUF-CMA\)
设存在\(SUF-CMA\)敌手,构造一个\(EUF-CMA\)
\[ \begin{align} &有(m_1,σ_1),(m_2,σ_2),(m_3,σ_3),……,(m_q,σ_q)\\ &敌手已经找到了(m^*,σ^*),已经通过了验证,\\ &那么(m^*,σ^*)≠\{(m_1,σ_1),(m_2,σ_2),(m_3,σ_3),……,(m_q,σ_q)\}\\ &由签名方案其签名算法是确定性的算法,得m^*≠\{m_1,m_2,m_3,……,m_q\}\\ &其实这就结束了,这就相当于构造出了一个EUF-CMA\\ &\\ \end{align} \]